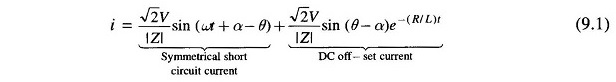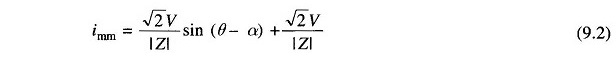Waveform of a Short Circuit Current on Transmission Line:
Let us consider the Short Circuit Current on Transmission Line. Certain simplifying assumptions are made at this stage.
- The line is fed from a constant voltage source (the case when the line is fed from a realistic synchronous machine).
- Short circuit takes place when the line is unloaded (the case of short circuit on a loaded line).
- Line capacitance is negligible and the line can be represented by a lumped RL series circuit.
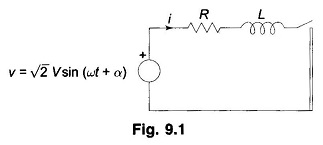
With the above assumptions the Transmission Line can be represented by the circuit model of Fig. 9.1. The short circuit is assumed to take place at t = 0. The parameter α controls the instant on the voltage wave when short circuit occurs. It is known from circuit theory that the current after short circuit is composed of two parts, i.e.
where
- is = steady state current
Thus short circuit current is given by
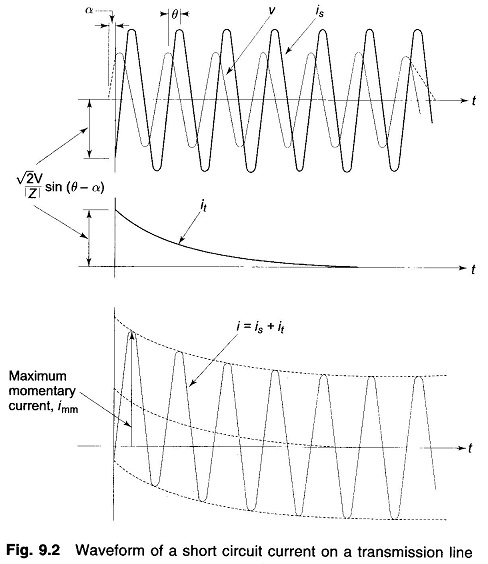
A plot of is, it and i = is + it is shown in Fig. 9.2. In power system terminology, the sinusoidal steady state current is called the symmetrical Short Circuit Current on Transmission Line and the unidirectional transient component is called the DC off-set current, which causes the total short circuit current to be unsymmetrical till the transient decays.
It easily follows from Fig. 9.2 that the maximum momentary short circuit current imm corresponds to the first peak. If the decay of transient current in this short time is neglected,
Since transmission line resistance is small, θ ≈ 90°.
This has the maximum possible value for α = 0, i.e. short circuit occurring when the voltage wave is going through zero. Thus
For the selection of circuit breakers, momentary Short Circuit Current on Transmission Line is taken corresponding to its maximum possible value (a safe choice).
The next question is ‘what is the current to be interrupted?’ As has been pointed out earlier, modem day circuit breakers are designed to interrupt the current in the first few cycles (five cycles or less). With reference to Fig. 9.2 it means that when the current is interrupted, the DC off-set (it) has not yet died out and so contributes to the current to be interrupted.
Rather than computing the value of the DC off-set at the time of interruption (this would be highly complex in a network of even moderately large size), the symmetrical Short Circuit Current on Transmission Line alone is calculated. This figure is then increased by an empirical multiplying factor to account for the DC off-set current.