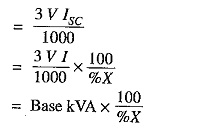Short Circuit kVA:

Although the potential at the point of fault is zero, it is a normal practice to express the short-circuit current in terms of Short Circuit kVA based on the normal system voltage at the point of fault.

The product of normal system voltage and short-circuit current at the point of fault expressed in kVA is known as Short Circuit kVA.

Let

V = normal phase voltage in volts

I = full-load current in amperes at base kVA

%X = percentage reactance of the system on base kVA upto the fault point

Short-circuit kVA for 3-phase circuit

i.e. Short Circuit kVA is obtained by multiplying the base kVA by 100/% X.

Reactor Control of Short-Circuit Currents:

With the fast expanding power system, the fault level (i.e. the power available to flow into a fault) is also rising. The circuit breakers connected in the power system must be capable of dealing with maximum possible short-circuit currents that can occur at their points of connection. Generally, the reactance of the system under fault conditions is low and fault currents may rise to a dangerously high value. If no steps are taken to limit the value of these short-circuit currents, not only will the duty required of circuit breakers be excessively heavy, but also damage to lines and other equipment will almost certainly occur.

In order to limit the short-circuit currents to a value which the circuit breakers can handle, addi­tional reactances known as reactors are connected in series with the system at suitable points. A reactor is a coil of number of turns designed to have a large inductance as compared to its ohmic resistance. The forces on the turns of these reactors under short-circuit conditions are considerable and, therefore, the windings must be solidly braced. It may be added that due to very small resistance of reactors, there is very little change in the efficiency of the system.

Advantages

• Reactors limit the flow of short-circuit current and thus protect the equipment from over­heating as well as from failure due to destructive mechanical forces.
• Troubles are localised or isolated at the point where they originate without communicating their disturbing effects to other parts of the power system. This increases the chances of continuity of supply.
• They permit the installation of circuit breakers of lower rating.