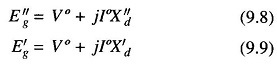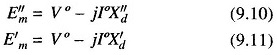Short Circuit Current of Loaded Synchronous Machine:
In the previous article on the Short Circuit of a Synchronous Machine, it was assumed that the machine was operating at no load prior to the occurrence of short circuit. The analysis of Short Circuit Current of Loaded Synchronous Machine is complicated. We shall, however, present here the methods of computing short circuit current when short circuit occurs under loaded conditions.
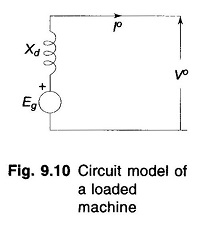
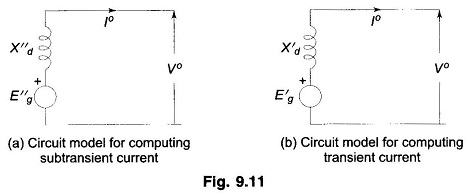
Figure 9.10 shows the circuit model of a Short Circuit Current of Loaded Synchronous Machine operating under steady conditions supplying a load current I° to the bus at a terminal voltage of V°. Eg is the induced emf under loaded condition and Xd is the direct axis synchronous reactance of the machine. When short circuit occurs at the terminals of this machine, the circuit model to be used for computing short circuit current is given in Fig. 9.11a for subtransient current, and in Fig. 9.11b for transient current. The induced emfs to be used in these models are given by
The voltage E″g is known as the voltage behind the subtransient reactance and the voltage E′g is known as the voltage behind the transient reactance. In fact, if I° is zero (no load case), E″g= E′g= Eg, the no load voltage, in which case the circuit model reduces.
Synchronous motors have internal emfs and reactances similar to that of a generator except that the current direction is reversed. During short circuit conditions these can be replaced by similar circuit models except that the voltage behind subtransient/transient reactance is given by
Whenever we are dealing with short circuit of an interconnected system, the synchronous machines (generators and motors) are replaced by their corresponding circuit models having voltage behind subtransient (transient) reactance in series with subtransient (transient) reactance. The rest of the network being passive remains unchanged.