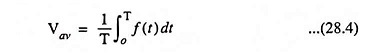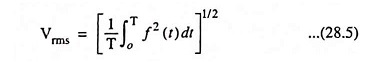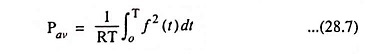Classification of Pulse Signals:
The Classification of Pulse Signals are divided into four categories, namely
- Periodic signals.
- Aperiodic signals.
- Random signals.
- Continuous and Discrete Signals
1. Periodic Signals:
Periodic signals are those which repeat themselves at regular intervals of time say ‘T’. This time ‘T’ is referred to as the time period. Sinusoidal signals, time-base signals and rectified waveforms (i.e., the output of the rectifier circuits) etc. fall under this category of pulse signals.
A periodic signal may be expressed as
where T is the time period.
Repetition frequency fR of a periodic signal is the reciprocal of the time period T. Thus
By iteration of Eq. (28.1) we have
where n is any integer i.e., n = 1, 2, 3 ….
The average value or mean value of a repetitive signal of periodic time T is given by the following expression
The rms value of a periodic or repetitive signal is given as
The instantaneous power, p is defined as
where v is the instantaneous voltage, i is the instantaneous current and R is the circuit resistance.
Thus average power of a voltage pulse is given as
Combining Eqs. (28.5) and (28.7) we have
2. Aperiodic Signals:
Aperiodic signals are those which occur only once in the entire time period (i.e., in the time interval from -∞ to +∞). Thus an aperiodic signal may be considered to be a periodic signal of infinite time period. Transients of different form constitute aperiodic signals. Since the aperiodic signals last for a short duration of time, our interest lies in storing it for analysis purpose. This may he accomplished by digital techniques i.e., amplitude and time quantization and digital storage.
3. Random Signals:
Random signals occur without any well defined mathematical description. At most such signals can be described by probabilistic models. Noise is one such random signal. A class of random signals which find applications in digital electronics is binary random signals. It is a two-valued random signal with random or unpredictable zero crossings. An example is a telegraph signal.
4. Continuous and Discrete Signals:
Pulse signals may be of two types, viz.; (i) continuous signal and (ii) discrete in time.
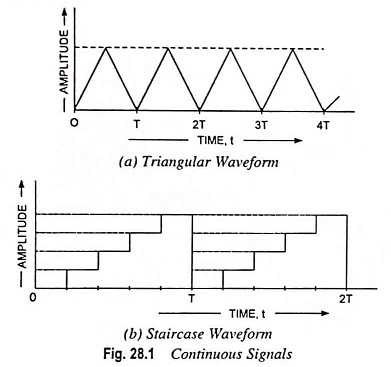
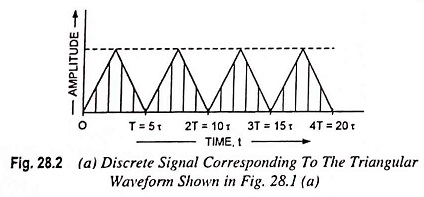
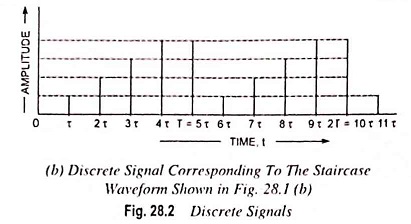
A continuous signal is one which is continuous function of independent variable “t” such as a triangular waveform or a staircase waveform, as depicted in Figs. 28.1 (a) and 28.1 (b) respectively. The signal must uniquely be defined at all values of time “t” within a given time range.
Discrete signal is defined only at a sequence of discrete values of independent variable “t”. In many practical situations the instants at which signals are defined are equally spaced and may be defined by t = t0 ± nτ where n takes only integral values (i.e., n = 1, 2, 3, …) and τ is the time duration between instants.
It is also possible to recover the original continuous signal from discrete signal. Discrete signals find wide applications in digital instrumentation, digital control systems and communications.