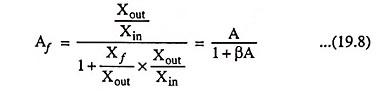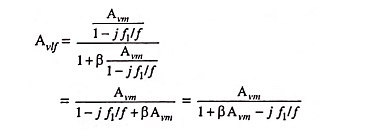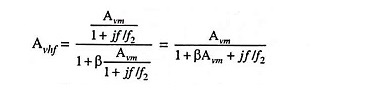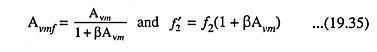Effect of Negative Feedback on Bandwidth:
The effect of negative feedback on bandwidth is given below as
From Eq. (19.8) voltage gain with feedback is given as
and from the above result it may be concluded that the voltage gain may be made to depend entirely on the feedback network. However, it is now important to consider the fact that even if β is constant, the voltage gain Av is not, since it depends on frequency. This means that at certain low or high frequencies βAv will not be much larger than unity, and, therefore, Eq. (19.26) will not be valid.
When negative feedback is applied in an amplifier, cutoff frequencies are also affected—lower cutoff frequency is lowered by a factor of (1 + βA) while upper cutoff frequency is raised by the same factor (1 + βA). This is explained below.
(i) Lower Cutoff Frequency f1: The voltage gain at a frequency f in low frequency range of R-C coupled amplifier is given as
where f1 is lower cutoff frequency and j j = √-1.
When negative feedback is applied
Substituting the value of Avl from Eq. (19.27) in Eq. (19.29) we have
By dividing numerator and denominator by 1 + β Avm, this equation may be rewritten as
where
From above equations we see that the midband amplification with feedback Avmf equals the midband amplification without feedback divided by 1 + βAvm. Also the lower cutoff frequency with feedback f′1 equals the lower cutoff frequency without feedback f1 divided by the same factor (1 + βAvm) i.e., lower cutoff frequency is reduced when negative feedback is applied.
(ii) Upper Cutoff Frequency: The voltage gain at frequency f in the high frequency range of R-C coupled amplifier is given as
When negative feedback is applied
Substituting the value of Avh from Eq. (19.32) in Eq. (19.33), we have
By dividing the numerator and denominator by 1 + βAvm, the above equation may be rewritten as
where
Thus we see that upper cutoff frequency with feedback equals the corresponding cutoff frequency without feedback f2 multiplied by the factor (1 + βAvm) i.e., upper cutoff frequency is raised when negative feedback is applied in an amplifier.
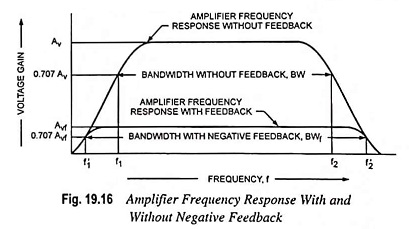
The effect of negative feedback on frequency response curve is shown in Fig. 19.16.
Bandwidth:
The effect of negative feedback on bandwidth is given as
Since f′2 > f2 and f′1 < f1 hence the negative feedback on bandwidth is increased.
Assuming f′2 >> f′1 and f2 >> f1 bandwidth may be rewritten
as
times bandwidth without feedback.
Thus we see that bandwidth of an amplifier with negative feedback is increased by the same factor by which voltage gain is reduced and gain bandwidth product remains the same. However, since the amplifier with feedback has lower gain, the net operation is to trade bandwidth for gain.