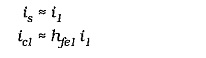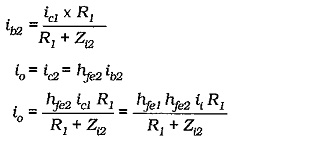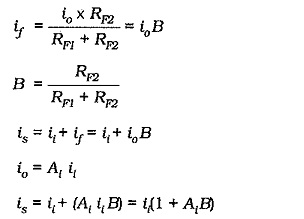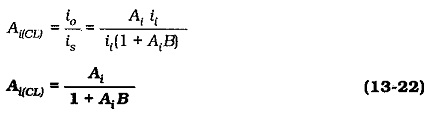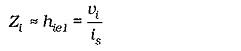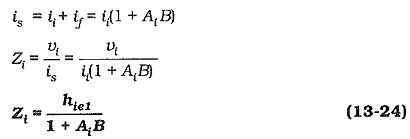Parallel Current Negative Feedback Circuit:

Current Feedback Circuit – In series-voltage feedback, a portion of the output voltage is fed back in series with the signal source. In Parallel Current Negative Feedback Circuit, a portion of the output current is fed back in parallel with the signal source. Just as series voltage feedback stabilizes the voltage gain of a circuit, so parallel current feedback stabilizes the current gain.

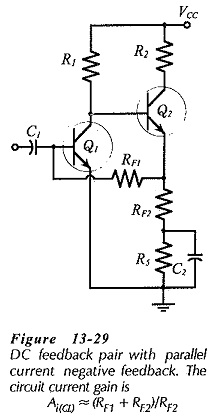
Consider the do feedback pair circuit in Fig. 13-29. An unbypassed resistor (R_F2) is connected in the emitter circuit of transistor Q₂, and Q₁ bias resistor (R_F1) is connected at the emitter terminal of Q₂. With this arrangement, any ac voltage developed across R_F2 is applied to R_F1.

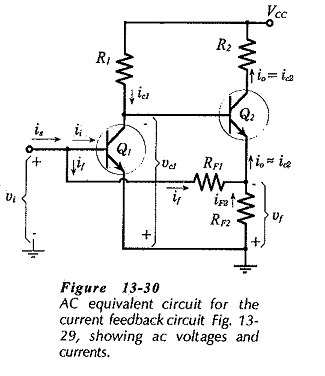
Look at the instantaneous polarities of the input voltage (v_i) and feedback voltage (v_f), as illustrated in the ac equivalent circuit in Fig. 13-30. When v_i is moving in a positive direction, v_c1 is negative-going. Because the emitter of Q₂ follows the voltage (v_c1) at its base, v_f (across R_F2) is also negative-going at this time.

Now look at the instantaneous ac current directions indicated in Fig. 13-30. When v_i goes positive, the signal current (i_s) flows into the circuit, and an input current (i_i) flows into the base of Q₁, as shown. Because v_f goes negative when v_f is positive-going, a feedback current (i_f) flows in R_F1 in the direction indicated, (from Q₁ base toward Q₂ emitter). Thus, some of the signal current is diverted away from the base of Q₁. This means that the output current (i_c2) is less than it would be if there was no current feedback, consequently, the circuit current gain is reduced.

Current Gain:

To determine the effect of negative feedback on the circuit current gain, first investigate the current gain without feedback, (the open-loop current gain). Suppose that R_F2 in Fig. 13-30 has a bypass capacitor connected across it, so that there is no negative feedback. Assuming that the resistance of R_F1 is very much larger than the Q₁ input impedance (h_ie1), virtually all of i_s enters the base of Q₁, (see Fig. 13-30).

i_c1 divides between R₁ and Z_i2. Using the current divider equation,

The open-loop current gain is,

Now derive an equation for the current gain with negative feedback. Referring to Fig. 13-30, it is seen that i_o (in the emitter circuit of Q₂) divides between R_F1 and R_F2, giving

The closed-loop current gain is,

If A_iB ≫ 1, then

It is seen that,

Parallel Current Negative Feedback Circuit stabilizes circuit current gain.

It should be noted that, in the current gain equations, the ac output current is taken as the current in the collector circuit of transistor Q₂. How this current divides between a capacitor-coupled external load (R_L) and the Q₂ collector resistor (R₃) depends on the values of R_L and R₃.

Output and Input Impedances:

In the circuit shown in Figs. 13-29 and 13-30, the Q₂ collector resistor (R₂) is outside the feedback loop. Therefore, like the case of emitter current feedback, the output impedance of this circuit is largely unaffected by feedback. (It can be shown that the impedance looking into the collector of Q₂ is increased by current feedback.) So, the circuit output impedance is, 

Assuming that R_F1 ≫ h_ie1, the circuit input impedance without feedback is,

As already shown, with negative feedback,

Therefore,

parallel current negative feedback reduces circuit input impedance by a factor of (1 + A_iB).

Although R_F1 is a bias resistor, it is also part of the feedback network, so it is not in parallel with the circuit input impedance.

Another way of looking at the circuit input impedance is in terms of the the feedback resistor R_F1 and the voltage gain of the first stage. It can be shown that,

Circuit Design:

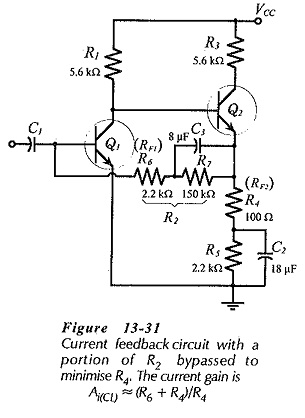
As with other negative feedback circuits, design of a Parallel Current Negative Feedback Circuit is approached by first ignoring the ac negative feedback components. Resistors R_F2 and R₅ in Fig. 13-29 are calculated as a single emitter resistor (R_E = R_F2 + R₅) to fulfill the desired dc conditions. Also, R_F1 is calculated (as for other dc feedback bias circuits) to provide the required base current to Q₁. R_F2 is then calculated from Eq. 13-23. Usually, the resistance of R_F1 is very large, and this results in a calculated resistance for R_F2 larger than (R_F2 + R₅). In this case, the base resistor for Q₁ should be made up of two resistors one of which is bypassed; see (R₂ = R_F1 + R₇) in Fig. 13-31. R_F1 is the unbypassed portion of R₂, and this is calculated in relation to R_F2.

Bypass capacitor C₂ (in Fig. 13-31) is calculated to give X_C2 = R_F2 at the desired lower cutoff frequency. Because the signal is derived from a current source, the impedance of the input coupling capacitor (C₁) at f₁ should be much smaller than the (normally-high) impedance of the signal source. Capacitor C₃ is determined by making X_C3 very much smaller than R_F1 at f₁.