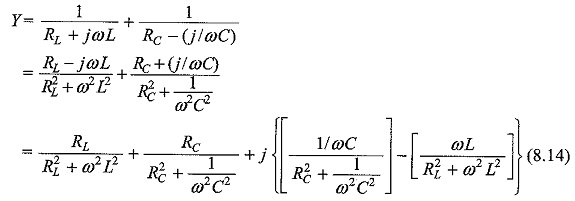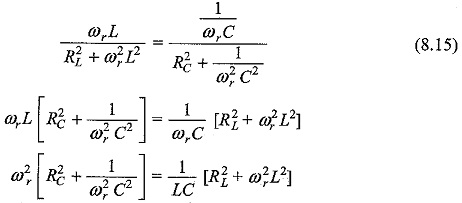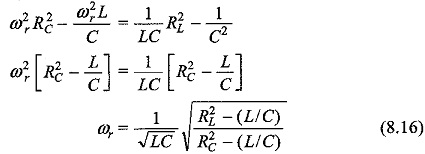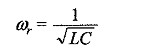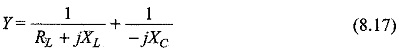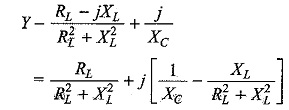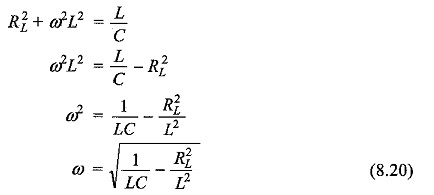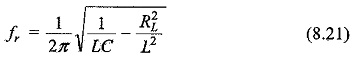Parallel RLC Circuit Resonance:

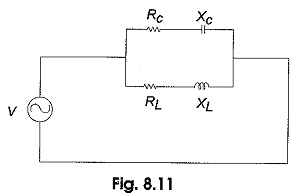
Parallel RLC Circuit Resonance – Basically, parallel resonance occurs when X_C = X_L. The frequency at which resonance occurs is called the resonant frequency. When X_C = X_L, the two branch currents are equal in magnitude and 180° out of phase with each other. Therefore, the two currents cancel each other out, and the total current is zero. Consider the circuit shown in Fig. 8.11.

The condition for resonance occurs when X_L = X_C.

In Fig. 8.11, the total admittance

At resonance the susceptance part becomes zero

The condition for resonant frequency is given by Eq. 8.16. As a special case, if R_L = R_C, then Eq. 8.16 becomes

Therefore

Resonant Frequency for a Tank Circuit:

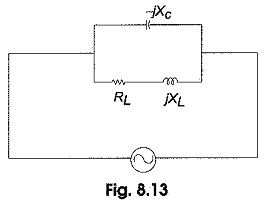
The Parallel RLC Circuit Resonance is generally called a tank circuit because of the fact that the circuit stores energy in the magnetic field of the coil and in the electric field of the capacitor. The stored energy is transferred back and forth between the capacitor and coil and vice-versa. The tank circuit is shown in Fig. 8.13. The circuit is said to be in resonant condition when the suscep­tance part of admittance is zero.

The total admittance is

Simplifying Eq. 8.17, we have

To satisfy the condition for resonance, the susceptance part is zero.

From Eq. 8.19, we get

The resonant frequency for the tank circuit is

Variation of Impedance with Frequency:

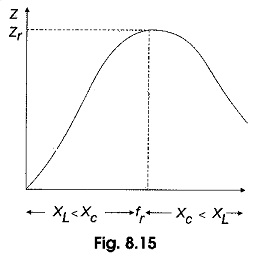
The impedance of a Parallel RLC Circuit Resonance is maximum at the resonant frequency and decreases at lower and higher frequencies as shown in Fig. 8.15.

At very low frequencies, X_L is very small and X_C is very large, so the total impedance is essentially inductive. As the frequency increases, the impedance also increases, and the inductive reac­tance dominates until the resonant frequency is reached. At this point X_L = X_C and the impedance is at its maximum. As the frequency goes above resonance, capacitive reactance dominates and the impedance decreases.