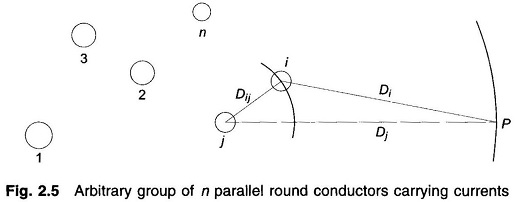
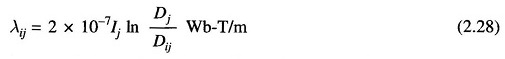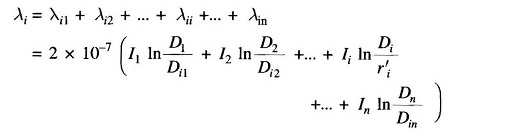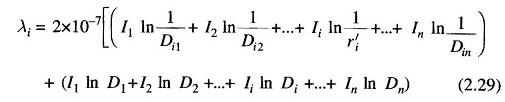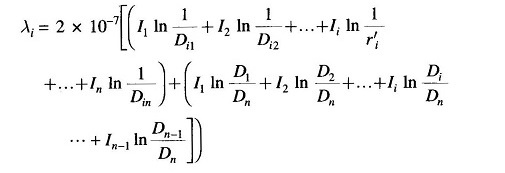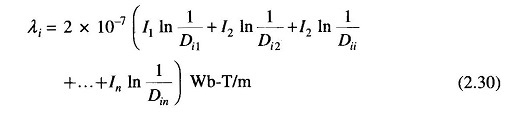Flux Linkage of n Parallel Conductors Carrying Current:
As shown in Fig. 2.5, consider a group of n parallel conductors carrying current I1, I2 ,…, In whose sum equals zero. Distances of these conductors from a remote point P are indicated as D1, D2 ,…, Dn. Let us obtain an expression for the total Flux Linkages of the ith conductor of the group considering flux up to the point P only.
The flux linkages of ith conductor due to its own current Ii (self linkages) are given by
The Flux Linkage of conductor i due to current in conductor j is
where Dij is the distance of ith conductor from jth conductor carrying current Ij. From Eq. (2.27) and by repeated use of Eq. (2.28), the total flux linkages of parallel conductors carrying current i due to flux up to point P are
The above equation can be reorganized as
But,
Substituting for In in the second term of Eq. (2.29) and simplifying, we have
In order to account for total flux linkages of conductor i, let the point P now recede to infinity. The terms such as In D1/Dn, etc. approach In 1 = 0. Also for the sake of symmetry, denoting r′i as Dii, we have