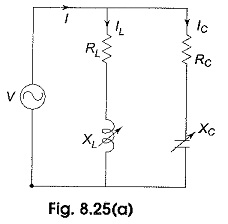
Locus Diagram of Parallel RLC Circuit:

(a) Variable X_L – Locus plots are drawn for parallel branches containing RLC elements in a similar way as for series circuits. Here we have more than one current locus. Consider the Locus Diagram of Parallel RLC Circuit shown in Fig. 8.25(a). The quantities that may be varied are X_L, X_C, R_L and R_C for a given voltage and frequency.

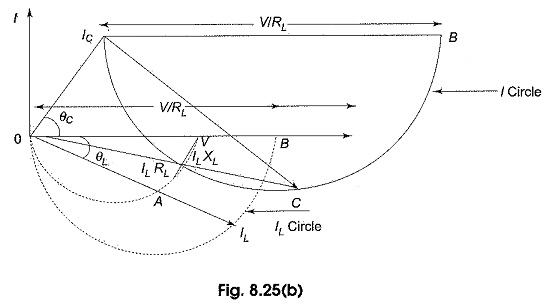
Let us consider the variation of X_L from zero to ∞. Let OV shown in Fig. 8.25(b), be the voltage vector, taken as reference. A current, I_C, will flow in the condenser branch whose parameters are held constant and leads V by an angle θ_C = tan^-1 (X_C/R_C), when X_L = 0, the current I_L, through the inductive branch is maximum and is given by V/R_L and it is in phase with the applied voltage.

When X_L is increased from zero, the current through the inductive branch I_L decreases and lags V by θ_L = tan^-1 X_L/R_L as shown in Fig. 8.25(b). For any value of I_L, the I_LR_L drop and I_LX_L drop must add at right angles to give the applied voltage. These drops are shown as OA and AV respectively. The locus of I_L is a semicircle, and the locus of I_LR_L drop is also a semicircle. When X_L = 0, i.e. I_L is maximum, I_L coincides with the diameter of its semicircle and I_LR_L drop also coincides with the diameter of its semi-circle as shown in the figure; both these semicircles are shown with dotted circles as OI_LB and OAV respectively.

Since the total current is I_C + I_L. For example, a particular value of I_C and I_L the total current is represented by OC on the total current semicircle. As X_L is varied, the locus of the resultant current is therefore, the circle I_C CB as shown with thick line in the Fig. 8.25(b).

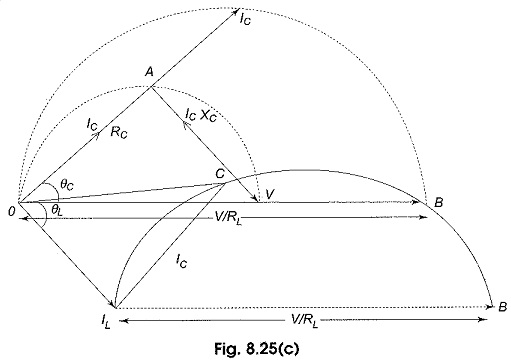
(b) Variable X_C – A similar procedure can be adopted as outlined above to draw the locus plots of I₁ and I when X_C is varying while R_L, R_C, X_L, V and f are held constant. The curves are shown in Fig. 8.25(c).

OV presents the voltage vector, OB is the maximum current through RC branch when X_L = 0; OI_L is the current through the R_L branch lagging OV by an angle θ_L = tan^-1 C_L/R_L.

As X_C is increased from zero, the current through the capacitive branch I_C decreases and leads V by θ_C = tan^-1 X_C/R_C. For a particular I_C, the resultant current I = I_L + I_C and is given by OC. The dotted semicircle OI_CB is the locus of the I_C, thick circle I_LCB is the locus of the resultant current.

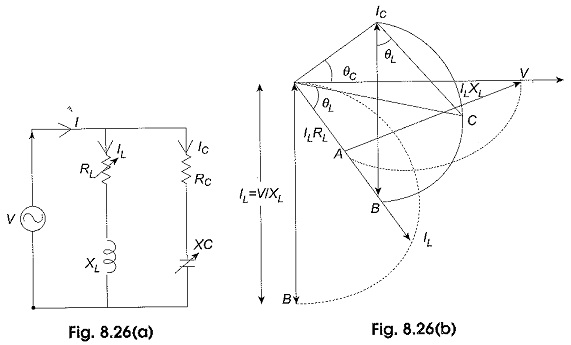
(c)Variable R_L – The locus of current for the variation of R_L in Fig. 8.26(a) is shown in Fig. 8.26(b). OV represents the reference voltage, OI_LB represents the locus of I_L and I_CCB represents the resultant current locus. Maximum I_L = V/X_L is represented by OB.

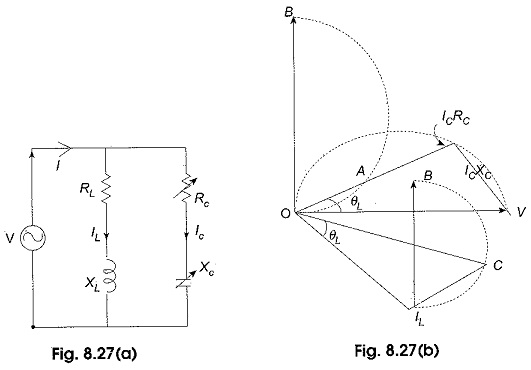
(d)Variable R_C – The locus of currents for the variation of R_C in Fig. 8.27(a) is plotted in Fig. 8.27(b) where OV is the source voltage and semicircle OAB represents the locus of I_C. The resultant current locus is given by BCI_L.