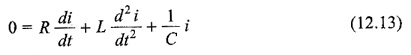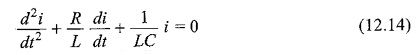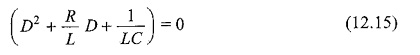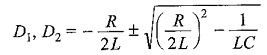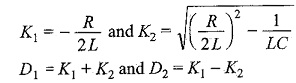Transient Response of RLC Circuit:

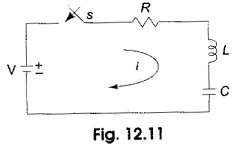
Consider a Transient Response of RLC Circuit consisting of resistance, inductance and capacitance as shown in Fig. 12.11.

The capacitor and inductor are initially uncharged, and are in series with a resistor. When switch S is closed at t = 0, we can determine the complete solution for the current. Application of Kirchhoff’s voltage law to the Transient Response of RLC Circuit results in the following differential equation.

By differentiating the above equation, we have

The above equation is a second order linear differential equation, with only complementary function. The, particular solution for the above equation is zero. Characteristic equation for the above differential equation is

The roots of Eq. 12.15 are

By assuming

Here K₂ may be positive, negative or zero.

K₂ is positive, when (R/2L)² > 1/LC

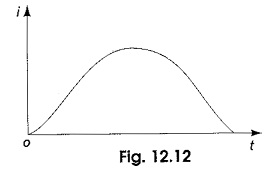
The roots are real and unequal, and give the over damped response as shown in Fig. 12.12. Then Eq. 12.14 becomes

The solution for the above equation is

i = c₁ e^(K1 ^{+ K}₂^)t + c₂ e^(K₁ ^{– K}₂^)t

The current curve for the over-damped case is shown in Fig. 12.12.

K₂ is negative, when (R/2L)² < 1/LC

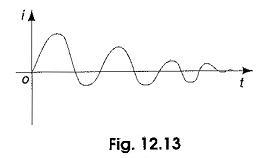
The roots are complex conjugate, and give the under-damped response as shown in Fig. 12.13. Then Eq. 12.14 becomes

The solution for the above equation is

The current curve for the under-damped case is shown in Fig. 12.13.

K₂ is zero, when (R/2L)² = 1/LC

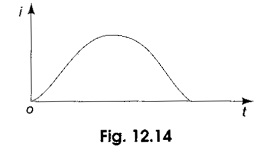
The roots are equal, and give the critically damped response as shown in Fig. 12.14. Then Eq. 12.14 becomes

The solution for the above equation is

The current curve for the critically damped case is shown in Fig. 12.14.