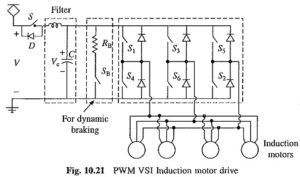
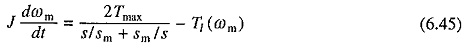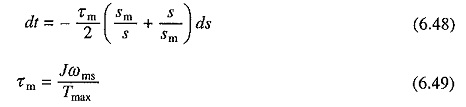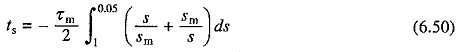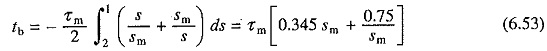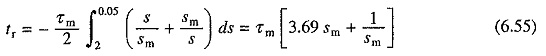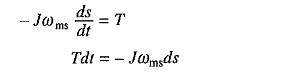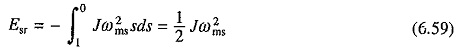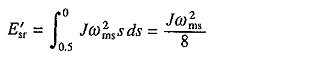Transient Analysis of Induction Motor:

Usefulness of analysis of transient operating conditions of a drive, e.g. starting, braking, load changing, speed changing, etc. is already explained. A rigorous analysis of transient operation of an induction motor drive, can be done only by the d-q axis model involving long calculations. A simple method of analysis, with satisfactory accuracy for most applications is obtained by using steady-state torque relations. Such an analysis is based on the assumption that electrical time constants can be neglected, as they are very small compared to mechanical time constant. Thus, we can write following equation for Transient Analysis of Induction Motor drive:

Equation (6.44) can.be evaluated graphically to obtain ω_m vs t curve, and energy losses in motor and external rotor resistance using the method already explained. This approach is general and can be employed for any Transient Analysis of Induction Motor as long as steady-state speed-torque curves of motor [T(ω_m)] and load [T₁(ω_m)] are known. Approximate analytical methods are presented below.

Starting and Plugging:

For starting and plugging operation of machine, torque is given by Eq. (6.15). Substituting from Eq. (6.15) into (6.44) yields

In some cases, Eq. (6.45) will be in integrable form, and therefore, can be solved analytically. It is useful to examine the transients for starting and plugging operations when operating on no load. Thus, from Eq. (6.45) for no load operation

Differentiating Eq. (6.3) gives

Substituting from Eq. (6.47) into (6.46) and rearranging the terms

τ_m is the mechanical time constant of motor. It is defined as the time taken by motor to reach its synchronous speed from standstill under constant accelerating torque equal to the maximum torque of the motor.

From Eq. (6.48), time required to start an induction motor on no load is

When operating on no load, steady-state is reached when s = 0. Thus during starting slip changes from 1 to 0. However, if (6.50) is integrated for s = 1 to s = 0 an infinite value is obtained for starting time. As explained, when final speed is the steady-state equilibrium speed, transients are considered to be over when 95% range of speed is covered. Therefore, in Eq. (6.50) integration is done from s = 1 to s = 0.05. Solving (6.50) gives

Thus starting time is a function of s_m. Starting time has a minimum value of 1.22τ_m at s_m = 0.4. From Eq. (6.12), when R_s is negligible, rotor resistance required to start the motor in minimum time is

From Eq. (6.48), time required for stopping by plugging, when initially running at synchronous speed, can be expressed as

Stopping time is again a function of s_m. It has a minimum value of 1.027τ_m at s_m = 1.47. Corresponding value of rotor resistance is

Similarly, from Eq. (6.48), time required for speed reversal by plugging when running on no load is given by

Minimum time for reversal is thus 2.88τ_m and corresponding value of s_m is 0.52. Rotor resistance required for speed reversal by plugging in minimum time is

Calculation of Energy Losses:

Let us next obtain expressions for energy loss in motor windings for starting and plugging operations. The rotor winding loss for starting can be written as

Substituting from Eqs. (6.5) and (6.11) gives

As the machine is operating under no load

Substituting from Eq. (6.47)

or

Substituting in (6.58) gives

It is interesting to note that rotor winding energy loss is equal to the kinetic energy stored in moving parts at completion of the starting process, and it is independent of the starting time or rotor resistance. However, if an external resistance is connected in rotor circuit only a part of this loss is used to heat the motor. Energy loss in stator winding, neglecting magnetizing current is

Hence, total winding loss during starting under no load is

Proceeding s milady, rotor winding loss during stopping by plugging under no load can be written as

Equation (6.59) suggests that rotor winding loss can be reduced when started by using methods based on the variation of synchronous speed. As an example let us consider a motor with an arrangement for doubling the pole number. Let it be started with higher pole number for which the synchronous speed is ω_ms/2. Then, from (6.59) rotor copper loss for change of speed from 0 to ω_ms/2 will be Jω²_ms/8. Now the pole number is lowered. Consequently, rotor copper loss for speed range ω_ms/2 to ω_ms will be

Thus, total rotor winding loss is Jω²_ms/4, which is one-half of the copper loss when there is no provision for doubling the pole number.