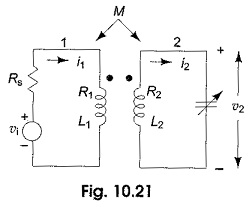
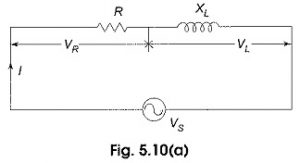
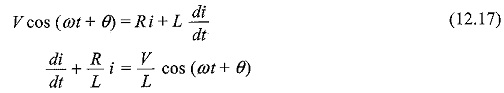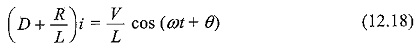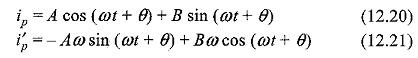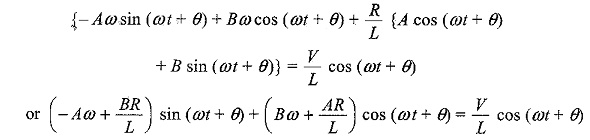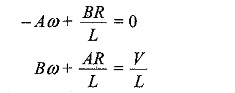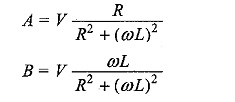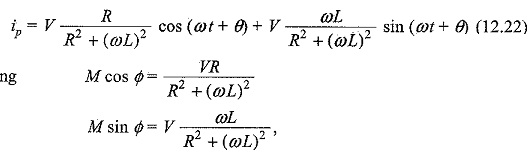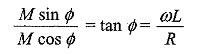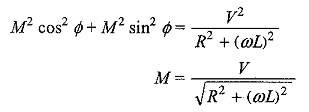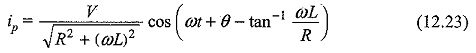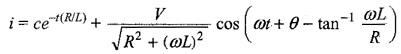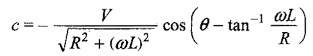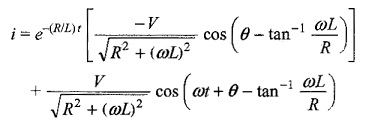Sinusoidal Response of RL Circuit:
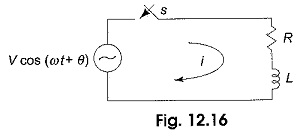
Consider a Sinusoidal Response of RL Circuit consisting of resistance and inductance as shown in Fig. 12.16.
The switch, S, is closed at t = 0. At t = 0, a sinusoidal voltage V cos (ωt + θ) is applied to the series R-L circuit, where V is the amplitude of the wave and θ is the phase angle. Application of Kirchhoff’s voltage law to the Sinusoidal Response of RL Circuit results in the following differential equation.
The corresponding characteristic equation is
For the above equation, the solution consists of two parts, viz. complementary function and particular integral.
The complementary function of the solution i is
The particular solution can be obtained by using undetermined co-efficients.
By assuming
Substituting Eqs 12.20 and 12.21 in Eq. 12.18, we have
Comparing cosine terms and sine terms, we get
From the above equations, we have
Substituting the values of A and B in Eq. 12.20, we get
to find M and Φ, we divide one equation by the other
Squaring both equations and adding, we get
The particular current becomes
The complete solution for the current i = ic + ip
Since the inductor does not allow sudden changes in currents, at t = 0, i = 0
The complete solution for the current is