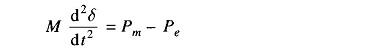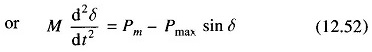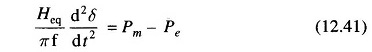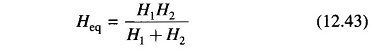Transient Stability in Power System:
Transient Stability in Power System – It has been shown already that the dynamics of a single synchronous machine connected to infinite bus bars is governed by the nonlinear differential equation
where
As said earlier, this equation is known as the swing equation. No closed format solution exists for swing equation except for the simple case Pm = 0 (not a practical case) which involves elliptical integrals. For small disturbance (say gradual loading), the equation can be linearized leading to the concept of steady state stability where a unique criterion of stability (∂Pe/∂δ>0) could be established. No generalized criteria are available for determining system stability with large disturbances (called transient stability) The practical approach to the Transient Stability in Power System problem is therefore to list all important severe disturbances along with their possible locations to which the system is likely to be subjected according to the experience and judgement of the power system analyst. Numerical solution of the swing equation is then obtained in the presence of such disturbances giving a plot of δ vs. t called the swing curve. If δ starts tc decrease after reaching a maximum value, it is normally assumed that the system is stable and the oscillation of δ around the equilibrium point will decay and finally die out. As already pointed out in the introduction, important severe disturbances are a short circuit or a sudden loss of load.
For ease of analysis certain assumptions and simplifications are always made (some of these have already been made in arriving at the swing equation (Eq. (12.52)).
All the assumptions are listed, below along with their justification and consequences upon accuracy of results.
- Transmission line as well as synchronous machine resistance are This leads to pessimistic result as resistance introduces damping term in the swing equation which helps stability.
- Damping term contributed by synchronous machine damper windings is This also leads to pessimistic results for the transient stability limit
- Rotor speed is assumed to be synchronous. In fact it varies insignificantly during the course of the Transient Stability in Power System.
- Mechanical input to machine is assumed to remain constant during the transient, i.e., regulating action of the generator loop is ignored. This leads to pessimistic results.
- Voltage behind transient reactance is assumed to remain constant, i.e., action of voltage regulating loop is ignored. It also leads to pessimistic results.
- Shunt capacitances are not difficult to account for in a stability study. Where ignored, no greatly significant error is caused.
- Loads are modelled as constant admittances. This is a reasonably accurate representation.
Note: Since rotor speed and hence frequency vary insignificantly, the network parameters remain fixed during a stability study.
A digital computer programme to compute the transient following sudden disturbance can be suitably modified to include the effect of governor action and excitation control.
Present day power systems are so large that even after lumping of machines (Eq. (12.17)), the system remains a multimachine one. Even then, a simple two-machine system greatly aids the understanding of the Transient Stability in Power System problem. It has been shown already that an equivalent single-machine infinite bus system can be found for a two-machine system (Eqs. (12.41) to (12.43)).
Upon occurrence of a severe disturbance, say a short circuit, the power transfer between machines is greatly reduced, causing the machine torque angles to swing relatively. The circuit breakers near the fault disconnect the unhealthy part of the system so that power transfer can be partially restored, improving the chances of the system remaining stable. The shorter the time to breaker operating, called clearing time, the higher is the probability of the system being stable. Most of the line faults are transient in nature and get cleared on opening the line. Therefore, it is common practice now to employ autoreclose breakers which automatically close rapidly after each of the two sequential openings. If the fault still persists, the circuit breakers open and lock permanently till cleared manually. Since in the majority of faults the first reclosure will be successful, the chances of system stability are greatly enhanced by using autoreclose breakers.
The procedure of determining the stability of a system upon occurrence of a disturbance followed by various switching off and switching on actions is called a stability study. Steps to be followed in a stability study are outlined below for a single-machine infinite bus bar system shown in Fig. 12.17. The fault is assumed to be a transient one which is cleared by the time of first recloser. In the case of a permanent fault, this system completely falls apart. This will not be the case in a multimachine system. The steps listed, in fact, apply to a system of any size.
- From prefault loading, determine the voltage behind transient reactance and the torque angle δ0 of the machine with reference to the infinite bus.
- For the specified fault, determine the power transfer equation Pe(δ) during In this system Pe = 0 for a three-phase fault.
- From the swing equation starting with δ0 as obtained in step 1, calculate δ as a function of time using a numerical technique of solving the nonlinear differential equation.
- After clearance of the fault, once again determine Pe (δ) and solve further for δ(t). In this case, Pe (δ) = 0 as when the fault is cleared, the system gets disconnected.
- After the transmission line is switched on, again find Pe (δ) and continue to calculate δ (t).
- If δ (t) goes through a maximum value and starts to reduce, the system is regarded as stable. It is unstable if δ (t) continues to increase. Calculation is ceased after a suitable length of time.