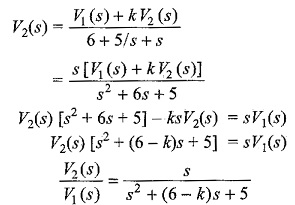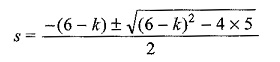Stability Criterion in Network Function:

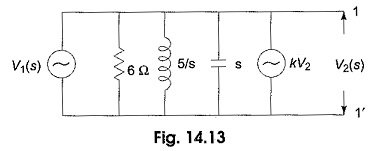
Stability Criterion – Passive networks are said to be stable only when all the poles lie in the left half of the s-plane. Active networks (containing controlled sources) are not always stable. Consider transformed active network shown in Fig. 14.13.

By applying Millman Theorem, we get

From the above transformed equation, the poles are dependent upon the value of k.

The roots of the equation are

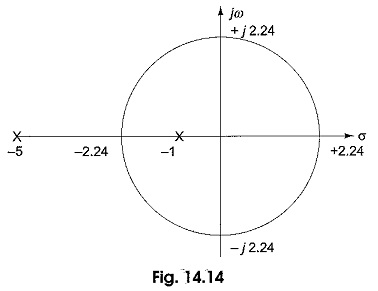
For k = 0, the poles are at —1, — 5, which lie on the left half of the s-plane. As k increases, the poles move towards each other and meet at a point √(6-k)²-20 =0, when k = 1.53 or 10.47. The root locus plot is shown in Fig.14.14.

The root locus is obtained from the characteristic equation s² + (6 — k)s + 5 = 0. As the value of k increases beyond 1.53, the locus of root is a circle. The poles are located on the imaginary axis at ± j2.24 for k = 6. At — 2.24, poles are coincident for k= 1.53 while at + 2.24, poles are coincident for k= 10.47.

When k>10.47, the poles again lie on the real axis but remain on the right half of the s-plane, one pole moving towards the origin and the other moving towards infinity From this we can conclude, as long as k is less than 6, the poles lie on the left half of the s-plane and the system is said to be stable. For k=6, the poles lie on the imaginary axis and the system is oscillatory in nature. For values of k greater than 6, the poles lie on the right half of the s-plane. Then the system is said to be unstable.