What is Crystalline Structure?
What is Crystalline Structure? – Solids are characterized by incompressibility, rigidity and mechanical strength. This indicates that the molecules, atoms or ions that make up a solid are closely packed, i.e., they are held together by strong forces and cannot move at random. On the contrary, gases are characterized by a high degree of compressibility. This is because in gases the molecules are having chaotic or random motion and exert little or no force on one another. Thus, while in gases we have ‘molecular chaos‘ , in solids we have well-ordered molecular arrangement.
Some solids, like sodium chloride, sulphur and sugar, besides being incompressible and rigid, have also characteristic geometrical forms. Such substances are said to be crystalline solids. The X-ray diffraction studies reveal that their ultimate particles (viz., molecules, atoms or ions) are arranged in a definite pattern throughout the entire three-dimensional network of the crystal. This definite and orderly arrangement of molecules, atoms or ions (as the case may be) extends over a large distance. This is termed as long-range order.
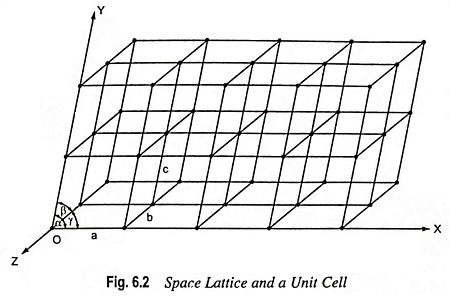
Crystal Lattice and Unit Cell: The position of atoms, molecules or ions in a crystal relative to one another in space, are designated usually by points. Such a representation is called space lattice or crystal lattice or crystalline structure. A crystal lattice is an array of points showing how molecules, atoms or ions are arranged at different sites in three-dimensional space.
An example of array of points in a three-dimensional space lattice is shown in Fig. 6.2, to illustrate the point. Each point represents an identical atom or group of atoms and this provides a crystalline structure.
The lattice points can be broken up into a number of unit cells. This is done by connecting the points by a regular network of lines, as illustrated in the Fig. 6.2. A unit cell is the smallest repeating unit in space lattice which when repeated over and over again results in a crystal of the given substance. Thus, space lattice of a crystal has been likened to a wallpaper on which single pattern is continuously repeated. Just as a pattern on the wallpaper is repeated again and again, similarly a unit cell (representing a definite pattern) is repeated again and again to build up a crystal. The only difference is that while wallpaper is in two dimensions, space lattice of a crystal is in three dimensions. The unit cell, in fact, is the smallest sample that represents the picture of the entire crystal. The crystal may be considered to consist of infinite number of unit cells. Each unit cell in a three-dimensional space has, evidently, three vectors, a, b and c, as shown in Fig. 6.2.
It should be clearly understood that these are the points and not the lines which constitute the space lattice or crystal lattice. The lines joining the points are drawn simply for representing three axes by means of which the relative positions of the points can be described. For example, in Fig. 6.2, three imaginary axes, OX, OY and OZ, which may be used to represent the unit cell, have been shown.
In order to describe a unit cell, we should know (i) the distances a, b and c, which give the lengths of the edges of the unit cell and (ii) the angles α, β and γ, which give the angle between the three imaginary axes OX, OY and OZ.