Nyquist Criterion:
Nyquist Criterion – This stability criterion enables one to establish the stability of a system using a graphical procedure in the frequency domain. Here also there is no necessity for the evaluation of the roots of the characteristic equation. The stability of a closed loop system is revealed by subjecting the open loop transfer function to a frequency response analysis. The stability criterion can be stated as
A closed loop control system is stable if the polar frequency locus of the systems open loop transfer function does not encircle the point (-1, 0) in a clockwise sense for all real values of frequency ω = ± ∞. If it encircles the point (-1,0) the system is unstable. If the locus passes through the point (-1, 0) the system is marginally stable, i.e., it is on the border line between stability and instability.
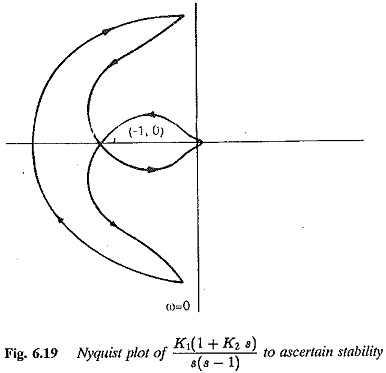
While drawing the Nyquist plot (polar frequency locus) it is sufficient to calculate the response for positive values of ω only, as ω changes from 0 to ∞. The plot for negative values of ω, i,e., as ω changes from 0 to —∞, is just a mirror image or conjugate of the above. However while establishing the system it is necessary to draw the complete locus for all frequency values varying from – ∞ to + ∞ (Fig. 6.19).
Application of the Nyquist Criterion:
In short, the following steps may be followed to apply the criterion to investigate the nature of stability of a closed loop system:
1.Obtain the open loop transfer function of the system.
2.Determine the frequency response plot of the function for positive values of ω starting from ω = 0 to ∞. The locus starts on the real x-axis and ends at the origin for minimum phase functions. If the transfer function contain factors of 1/s, 1/s2, the locus starts at ∞ on the real axis for ω = 0 and swings through ±90° to reach the appropriate axis for ω = 0+.
3.Draw the mirror image of the locus which gives the locus for the frequency in the range ω = —∞, 0.
4.If the locus encircles the point (-1, 0) the system is unstable. The system is on the boundary stability if the locus passes through (-1, 0).
Features of the Nyquist Criterion:
1.The stability as well as performance of a closed loop system can be investigated using open loop data and a simple graphical procedure. The use of an open loop transfer function is simpler than the use of a corresponding closed loop transfer function.
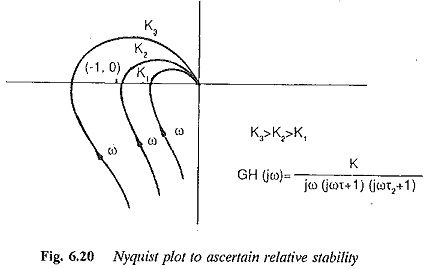
2.The method can be used to ascertain the relative stability of the system (Fig. 6.20). This enables one to improve both the transient and steady-state responses by properly adjusting the parameters of the system.
3.Only a few points on the locus need to be calculated. The full plot of the locus can be drawn using these values. It is often necessary and sufficient if the locus near the point (-1, 0) is drawn.
4.For minimum phase functions the locus starts on the real axis for ω = 0 and ends at the origin for ω = – ∞.
5.The Nyquist plot can be very simply sketched if the transfer function has no terms containing s in the numerator. A pole or a factor in the denominator of nature s or (1 + sr) causes a rotation of the locus by —90°. One or more such factors in the denominator tend to make the system unstable. Based on these considerations the first and second order system are never unstable.
6.The Nyquist plot of a transfer function having s factors in the numerator not continually change with continuous change in ω. However a factor of the nature or (1 + sr) in the numerator has the effect of nullifying the effect of a similar factor in the denominator by contributing or rotating the frequency by +90°.
7.The application of Nyquist Criterion to a system also reveals the number of roots on the right hand side of the 3-plane. This is given by the number of times the Nyquist locus encircles the (-1, 0) point.
8.However, for complicated systems, sometimes the encirclement of the point by the locus is not directly obvious. The following procedure may be used to check whether the locus has encircled the point (-1, 0).
(a)Draw a line in any direction from (-1,0) to intersect the locus.
(b)Put an arrow on the locus touching the line in the direction of locus ascertained in the sense of 0+ to ∞+ at each intersecting point.
(c)If the number of anticlockwise arrows and clockwise arrows are equal, it may be concluded that the locus does not encircle the point (-1, 0), otherwise the point (-1, 0) is encircled and the system is unstable.