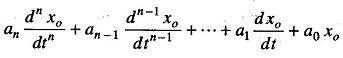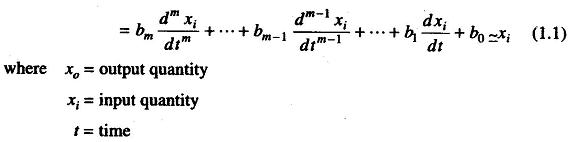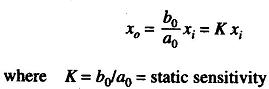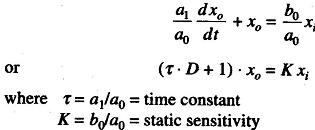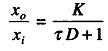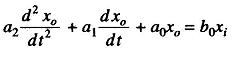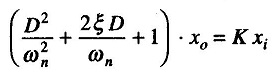Dynamic Characteristics:
Instruments rarely respond instantaneously to changes in the measured variables. Instead, they exhibit slowness or sluggishness due to such things as mass, thermal capacitance, fluid capacitance or electric capacitance. In addition to this, pure delay in time is often encountered where the instrument waits for some reaction to take place. Such industrial instruments are nearly always used for measuring quantities that fluctuate with time. Therefore, the Dynamic Characteristics and transient behavior of the instrument is as important as the static behavior.
The Dynamic Characteristics of an instrument is determined by subjecting its primary element (sensing element) to some unknown and predetermined variations in the measured quantity. The three most common variations in the measured quantity are as follows:
1. Step change, in which the primary element is subjected to an instantaneous and finite change in measured variable.
2. Linear change, in which the primary element is following a measured variable, changing linearly with time.
3. Sinusoidal change, in which the primary element follows a measured variable, the magnitude of which changes in accordance with a sinusoidal function of constant amplitude.
The dynamic characteristics of an instrument are
- speed of response,
- fidelity,
- lag, and
- dynamic error.
1. Speed of Response
It is the rapidity with which an instrument responds to changes in the measured quantity.
2. Fidelity
It is the degree to which an instrument indicates the changes in the measured variable without dynamic error (faithful reproduction).
3. Lag
It is the retardation or delay in the response of an instrument to changes in the measured variable.
4. Dynamic Error
It is the difference between the true value of a quantity changing with time and the value indicated by the instrument, if no static error is assumed.
When measurement problems are concerned with rapidly varying quantities, the dynamic relations between the instruments input and output are generally defined by the use of differential equations.
Dynamic Response of Zero-order Instruments:
We would like an equation that describes the performance of the zero order instrument exactly. The relations between any input and output can, by using suitable simplifying assumptions, be written as
a’s and b’s are combinations of systems physical parameters, assumed constant.
When all the a’s and b’s, other than a0 and b0 are assumed to be zero, the differential equation degenerates into the simple equation given as
Any instrument that closely obeys Eq. (1.2) over its intended range of operating conditions is defined as a zero-order instrument. The static sensitivity (or steady state gain) of a zero-order instrument may be defined as follows
Since the equation xo = Kxi is an algebraic equation, it is clear that no matter how xi might vary with time, the instrument output (reading) follows it perfectly with no distortion or time lag of any sort. Thus, a zero-order instrument represents ideal or perfect dynamic performance. A practical example of a zero order instrument is the displacement measuring potentiometer.
Dynamic Response of a First Order Instrument:
If in Eq. (1.1) all a’s and b’s other than a1, a0, b0 are taken as zero, we get
Any instrument that follows this equation is called a first order instrument. By dividing by a0, the equation can be written as
The time constant τ always has the dimensions of time while the static sensitivity K has the dimensions of output/input. The operational transfer function of any first order instrument is
A very common example of a first-order instrument is a mercury-in-glass thermometer.
Dynamic Response of Second Order Instrument:
A second order instrument is defined as one that follows the equation
The above equations can be reduced as
Any instrument following this equation is a second order instrument. A practical example of this type is the spring balance. Linear devices range from mass spring arrangements, transducers, amplifiers and filters to indicators and recorders.
Most devices have first or second order responses, i.e. the equations of motion describing the devices are either first or second order linear differentials. For example, a search coil and mercury-in-glass thermometer have a first order response. Filters used at the output of a phase sensitive detector and amplifiers used in feedback measuring systems essentially have response due to a single time constant. First order systems involve only one kind of energy, e.g. thermal energy in the case of a thermometer, while a characteristic feature of second order system is an exchange between two types of energy, e.g. electrostatic and electromagnetic energy in electrical LC circuits, moving coil indicators and electromechanical recorders.