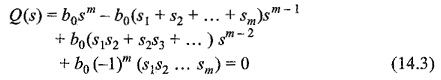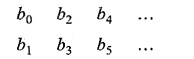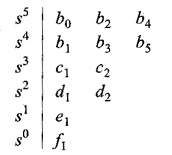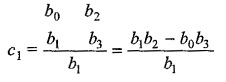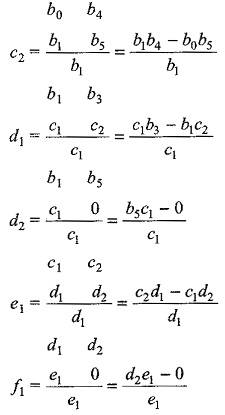Routh Criterion:

Routh Criterion – The locations of the poles gives us an idea about stability of the active network. Consider the denominator polynomial

To get a stable system, all the roots must have negative real parts. There should not be any positive or zero real parts. This condition is not sufficient. Let us consider the polynomial

In the above polynomial, though the coefficients are positive and real, the two roots have positive real parts. From this we conclude that the coefficients of Q(s) being positive and real is not a sufficient condition to get a stable system. Therefore, we have to seek the condition for stability which is necessary and sufficient.

Consider the polynomial Q(s) = 0. After factorisation, we get

On multiplication of these factors, we get

Equating the coefficients of Eqs 14.1 and 14.3, we have

If all the roots have negative real parts, then from the above equations it is clear that all the coefficients must have the same sign. This condition is not sufficient due to the fact that the zero value of a coefficient involves cancellation, which requires some root to have positive real parts.

The Routh criterion for stability is discussed below. Consider a polynomial

Taking first row coefficients and second row coefficients separately, we have

Now we complete the Routh array as follows.

For m = 5

where c₁,c₂,d₁,d₂,e₁,f₁ are determined by the algorithm given below.

In order to find out the element in kth row and jth column, it is required to know the four elements. These elements in the row (k — 1) and row (k — 2) just above the elements are in column 1 of the array and (J + 1) column of the array. The product of the elements joined by a line with positive slope has positive sign while the product of elements joined with a line with negative slope has a negative sign. The difference of these products is divided by the element of column 1 and row (k — 1). The above process is repeated till m + 1 rows are found in the Routh array.

According to the Routh-Hurwitz theorem, the number of changes in the sign of the first column to the right of the vertical line in an array moving from top to bottom is equal to the number of roots of Q(s) = 0 with positive real parts. To get a stable system, the roots must have negative real parts.

According to the Routh-Hurwitz criterion, the system is stable, if and only if, there are no changes in signs of the first column of the array. This requirement is, both the necessary and sufficient condition for stability.