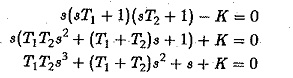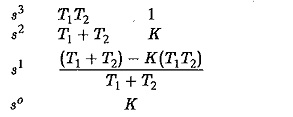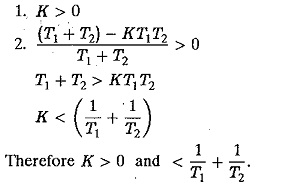Routh Hurwitz Criterion:

The Routh Hurwitz Criterion states that the system is stable if the Routh table has no negative elements in the first column. The roots of the characteristic polynomial are negative if they are real or contain negative real parts if the elements of the first column of the Routh Table are positive. The negative elements indicate positive real roots or roots with positive real parts. The number of changes in the sign of the first column actually indicate the number of roots on the right hand side of the s-plane.

Using this method the stability of a linear system can be investigated very easily and quickly. It also indicates the number of roots, if any, on the right hand side of the s-plane. However, the method does not provide any infor­mation regarding the relative stability of the system. The method can be used to select the parameters which would make the system stable, mostly the gain constant of the system. In the case of controlled variable frequency drives this can be used to study the effect of variation of parameters on the stability of the drive system.

Before applying the stability criterion to the characteristic equation, the first and foremost condition to be satisfied is that all the coefficients of the characteristic equation are present and positive. If any coefficient is missing or is negative, positive roots may occur.

The coefficients of the characteristic equation are used to write down the first two rows of the Routhian array using alternate powers of s, in the order of descending powers. The missing terms are represented by zeros. These zeros cause sign changes in the first column indicating positive roots or complex roots with a positive real part. These two rows are used to build the complete array. The arithmetic manipulations in the development of the array may be made easier by dividing any row by a constant. The array is developed until a row of zeros appears, after a systematic formation of zeros in a step pattern in pairs. If the row of zeros appears before the array is complete, the subsidiary equation before the row of zeros is differentiated and substituted for the row of zeros. If the intermediate rows of the array has a zero in the first column, it presents a problem in developing the subsequent rows. This difficulty is overcome by multiplying the characteristic equation by (s + K). This does not alter the situation because s = – K is a negative root.

The application of the Routh Hurwitz Criterion is discussed in the following by means of an example.

Example

The open-loop transfer function of a unity feedback control system is given

Use Routh Hurwitz Criterion to establish a relation between K,T₁,T₂ so that the system is stable.

Solution:

The characteristic equation of the system is

The Routh Hurwitz Criterion array is

For the system to be stable