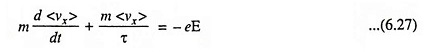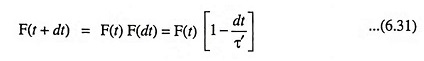Relaxation Time, Collision Time and Mean Free Path:

The relaxation time is closely related to the mean time of flight between collision and also to the mean free path of the conduction electrons, which is the average distance of undisturbed motion between collision. All the collision processes occurring in the electron gas may be explained through relaxation time. The collisions are caused by thermal or structural imperfections in the lattice. The relaxation time is introduced as the characteristic time governing the establishment of equilibrium, through collision, from an initial disturbed situation in which v_x ≠ 0.

The relaxation time is mathematically understood as follows:

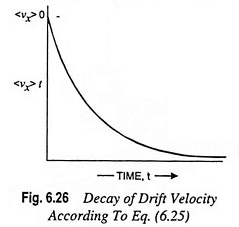
Let the electrons in a metal have an average velocity <v_x> 0 at any instant, t = 0; given that for t > 0 there is no external field, the electrons interact only with the lattice and ultimately the average velocity will go to zero. At any instant t(> 0), let the velocity be given by the expression (Fig. 6.26)

where τ is the relaxation time of electrons.

The rate of change of velocity due to collision becomes

The subscript “coll” refers to collisions carried out by the electrons with the lattice.

Equation (6.25) is the solution of a modified equation of motion of electrons if we consider the frictional forces due to collisions.

Considering the relaxation time, the frictional force on the electrons due to collision may be expressed as m <v_x>/τ. Hence, the modified equation of electrons becomes

In the absence of the external forces (– eE), the free motion satisfies

Or, if <v_x> 0 is the initial drift velocity in the non-equilibrium distribution, the approach to the equilibrium is described by the appropriate solution of Eq. (6.28)

The disturbances from equilibrium die out exponentially.

Let us now consider the collisions from the point of view of time. Assume that the probability for an electron to collide with a lattice (obstacle) during a short time interval dt is given by dt/τ′, where τ′ is a constant with the dimensions of time. Let F(t) represent the probability that an electron moves for a time t without suffering a collision, and let F(t + dt) represent the same probability for a period (t + dt). We may now write

and from probability theory

Comparing Eqs. (6.30) and (6.31), we have

Since F(t) = 1 for t = 0 which fixes the integration constant. The average time which elapses between collisions is given as

because -dF/dt gives the probability that the electron collides between t and (t + dt). Substituting F(t) from Eq. (6.32) in Eq. (6.33), we have

Hence, the physical meaning of τ′ introduced in the proba­bilities above is that it represents the average time of collisions.

For isotropic materials, the mean time of collision is the same as the relaxation time, i.e., τ′ = τ. This is not true for non-isotropic materials.

The mean free path of an electron, λ, will be defined as

where v is an appropriate average velocity of electron. In the case of metals, the conductivity always refers to a single total velocity, the one corresponding to Fermi energy. We know that free electrons in a metal can accept a series of discrete energy levels. At absolute zero, all energy levels below a certain value E_F are filled, and those above E_F being empty, E_F is called the Fermi level of electrons. The magnitude of E_F is of the order of several electron volts. At any temperature T, the probability of a state corresponding to the energy E being occupied by an electron is given as

where k is Boltzmann’s constant.

The velocity of an electron with Fermi energy, v_F is given as

Thus mean free path,