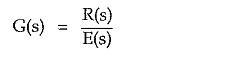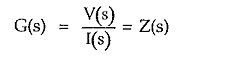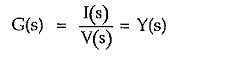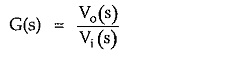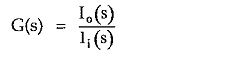Transfer Function or Network Function:

Every network is designed to produce a particular output, when input is applied to it. The network performance is judged by studying its output for the applied input. The output is the effect of network parameters on the applied input. Thus once the network is designed, the effect of network parameters remains same, on the input to produce the output. The effect of network parameters is mathematically expressed in s domain which is called network function, system function or transfer function of the network. It is the characteristics of the network and once known for any type of applied input, the output can be predicted. Let us see mathematical definition of the network function.

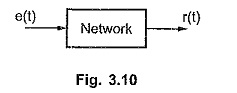
Consider a network shown in the Fig. 3.10.

e(t) = Input or excitation

r(t) = Output or response

The network function is defined as the ratio of Laplace transform of output (response) of the network to the Laplace transform of the input (excitation) applied to the network, under the assumption that all initial conditions are zero.

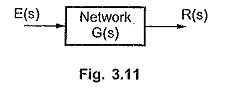
The network function is denoted as H(s), G(s) or T(s) in s domain. The network can be represented interms of network function as shown in the Fig. 3.11.

Thus the network function is defined as,

The R(s) and E(s) are the Laplace transforms of r(t) and e(t). Once network function G(s) is known, the output for any type of input can be obtained. But to determine the network function, the output terminals must be specified.

Properties of Transfer Function:

The various properties of transfer function are,

• It is a mathematical model of the network explaining the operation which network performs on the input to produce the output.
• It is the characteristics of the network and is unique for given set of input and output variables.
• It is independent of the magnitude and nature of the input.
• For any input applied, the output of the network can be predicted from the Network Function.
• Initial conditions loose the importance while obtaining the Network Function.
• The transfer function does not provide any information regarding the physical structure of the system or network.
• The time domain differential equation relating input and output describing the network can be easily obtained from the Network Function. Thus the Network Function gives a full description of the dynamic characteristics of the network. The excitation and the response of the network may be currents or voltages. Hence the network function G(s) may represent impedance function, admittance function, voltage ratio transfer function or current ratio transfer function.

1.Impedance:

When the excitation is current and the response is voltage then the network function represents impedance function

2.Admittance:

When the excitation is voltage and the response is current then the network function represents admittance function.

3.Voltage ratio transfer function:

When the excitation and response both are voltages then the network function represents voltage ratio transfer function.

where V_o = Response and V_i = Excitation

4.Current ratio transfer function:

When the excitation and response both are currents then the network function represents current ratio transfer function.

where   I_o = Response and I_i = Excitation