Frequency Response Transfer Function:
The previous sections- show that with the time response of a system, even though it is a direct method of analysis, the adjustment of the parameters to give a satisfactory time domain performance is rather tedious particularly with higher order systems. On the other hand methods utilising Frequency Response Transfer Function are extremely easy and practical for the analysis and synthesis of control systems. The Frequency Response Transfer Function is defined as the steady-state response of the system for sinusoidal excitation over a range of frequencies. It is well known, that sinusoidal excitation offers advantages in the analysis that, in a linear system, the output or signal at any other point of the system is sinusoidal; however it differs from the input signal in phase and magnitude.
The Frequency Response Transfer Function method has the following advantages:
1.The experimental determination of frequency response of a system is very easy, because sinusoidal signal of varying frequencies and amplitudes are readily available. The method is reliable and uncomplicated for the experimental analysis of a system. This data can be used to formulate the transfer function of the system. The frequency response provides information regarding the response of the system to noise and disturbance. Bandwidth can be controlled. The system can be designed so that the effects of these are minimum.
2.The transfer function describing the frequency response is very easily obtained by substituting jω for s in its transfer’ function in s It is a complex function of ω having real and imaginary parts. It has a magnitude and phase, the plot of which gives the frequency response of the system.
3.One such plot is the Nyquist plot which gives the absolute and relative stabilities of the closed loop system response from the knowledge of the open loop frequency response. The actual roots of the system need not be
4.Design methods in the frequency domain are simple.
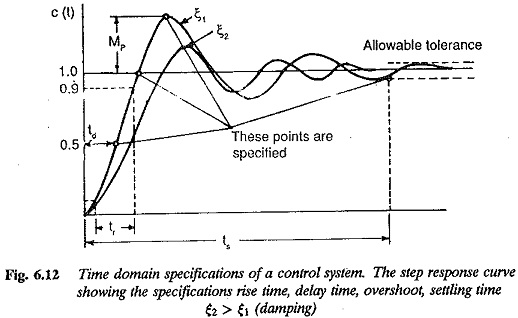
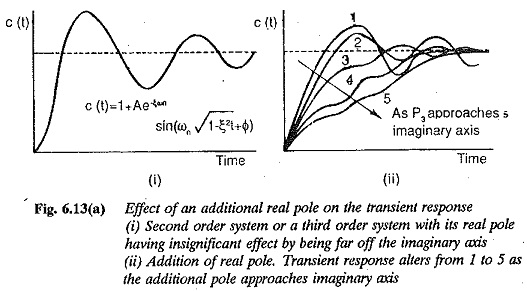
However to design a control system in the frequency domain satisfying the given time domain specifications, a correlation between the time response and Frequency Response Transfer Function is necessary. There is no such direct correlation except for second order system. While designing a closed loop system we may adjust the frequency response characteristics by using several design criteria in order to obtain the desired transient or time response.
In order to utilise the frequency response approach effectively, it is necessary to understand the indirect correlation between the transient and frequency response. The indirect correlation actually interprets the desired dynamic response in terms of the frequency response characteristic. Changes are made in the frequency response, so that the modified one gives the desired time response.