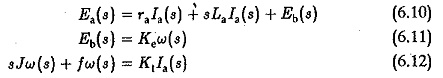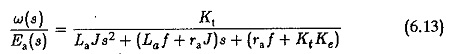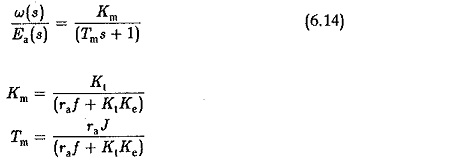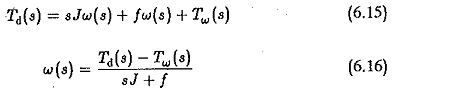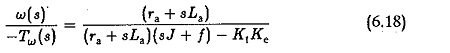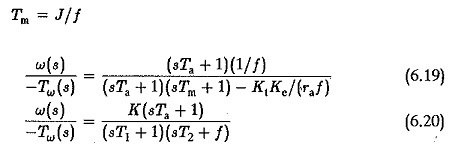Transfer Function of Armature Controlled DC Motor:

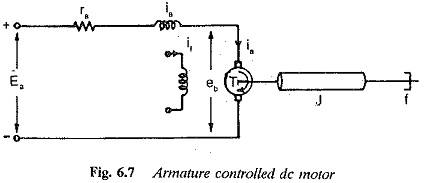
The speed of a dc motor can be controlled by varying the voltage applied to the armature of a dc motor. A separately excited dc motor with variable armature voltage finds application as a drive motor in a variable speed drive. The variable armature voltage is provided by a phase controlled rectifier. The schematic of an Transfer Function of Armature Controlled DC Motor is shown in Fig. 6.7.

The torque developed by the dc motor

where

Φ is air gap flux

i_a is armature current

K is a constant

Neglecting the affects of saturation and armature reaction we have the air gap flux proportional to the field current. That is

Because i_f is constant the torque developed is given by

where K_t is motor constant. The armature voltage e_a is supplied by the thyris­tor converter. The armature circuit equation is given by

e_b in Eq. 6.7 is the rotational (back) emf induced in the armature and is proportional to the product of speed and flux. But, the flux of the motor is constant. Therefore, The dynamic equation of the motor giving the torque balance can be written as

Assuming the initial conditions to be zero, Laplace transforms of Eqs 6.7, 6.8 and 6.9 can be written as

Taking E_a(s) as the input and w(s) as the output, the transfer function w(s)/E_a(s) can be obtained by eliminating l_a(s) from the equations and is given by

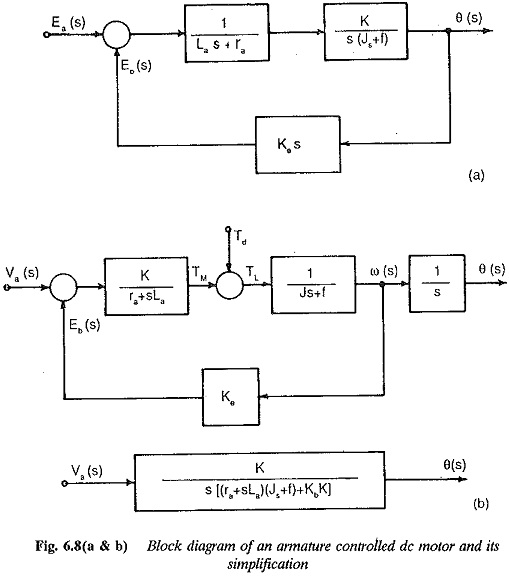
The block diagram given in Fig. 6.8(a) represents Eq. 6.13. This can be finally reduced to a single block given in Fig. 6.8(b).

Normally the armature inductance L_a is very small and may be neglected. The transfer function in this case is given by

It can be seen that the back emf affects the damping of the system. A transfer function between the speed and load torque can be derived by assuming the other input e_a to be zero. In this case the dynamic equation would be

But from Eqs 6.10 and 6.11 we have

Substituting in Eq. 6.15 and simplifying we get

where K is constant. If the poles of this transfer function are complex conju­gates the speed change for a change in the load torque is oscillatory.