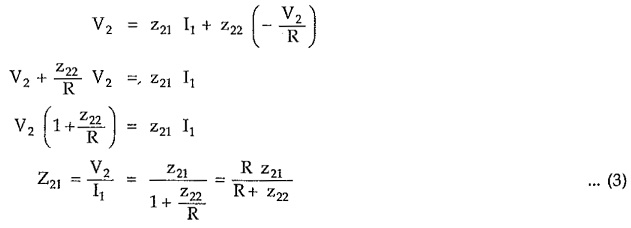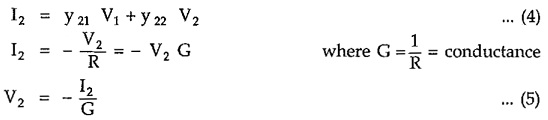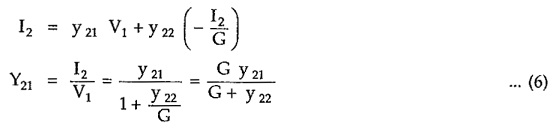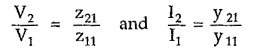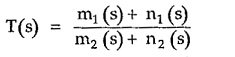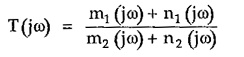Elements of Transfer Function Synthesis:

A transfer function is generally defined to specify the properties of a two port network. Hence Elements of Transfer Function Synthesis is also known as two port synthesis.

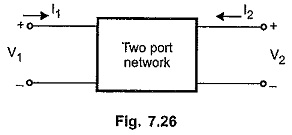
Consider a two port network as shown in the Fig. 7.26.

V₁ and I₁ are voltage and current at port 1 while V₂ and I₂ are voltage and current at port 2.

Thus there are four variables associated with the network, the two are voltage variables V₁, V₂ and other two are current variables I₁ and I₂.

A ratio of voltage or current at one port to the voltage or current at the other port is called a transfer function of the network.

The following transfer functions can be defined for the two port network,

A two port network is generally defined by its parameters such as z parameters and y parameters.

In the transfer function synthesis, the two port network is terminated at port 2 in resistance R. Let us express the transfer impedance and admittance functions of a two port terminated network, in terms of z and y parameters.

Note that the transfer functions are denoted by capital letters while the network parameters are denoted by small letters.

Transfer Functions of Two Port Terminated Network:

Consider a two port network, terminated in resistance R as shown in the Fig. 7.27.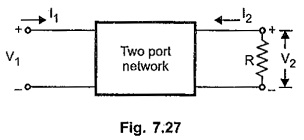

Z₂₁ = V₂/V₁ = Transfer impedance function

From the z parameters we can write,

Substituting in (1),

The transfer impedance function Z₂₁ is denoted as capital letter while z₂₁, z₂₂ are the z parameters, denoted by small letters.

Now

Y₂₁ = I₂/V₁ = Transfer admittance function

From the y parameters we can write,

Substituting in (4),

Similar to impedance and admittance functions, the other transfer functions can also be expressed in z and y parameters.

The results are helpful in the synthesis of two port networks

Properties of Transfer Functions:

The transfer function is the ratio of two polynomials in s.

It is denoted as T(s).

The T(s) is the transfer function of linear network consisting of lumped bilateral passive elements. The properties of such T(s) are,

1. The T(s) is real when s is real.

When T(s) is rational with real coefficients, then this property gets satisfied.

2. The poles of T(s) are simple having zero or negative real parts. T(s) has no poles in right half of s plane.
3. The T(s) has no multiple poles on the jω axis.
4. The degree of polynomial N(s) can not exceed the degree of the polynomial D(s) by more than one.
5. The polynomial D(s) must be Hurwitz polynomial.
6. The T(s) can be split into odd and even parts as,

where m₁, m₂ are even parts and n₁, n₂ are odd parts of N(s) and D(s) respectively.

Replacing s by jω we get,

From T(jω) the amplitude and phase response of T(s) can be obtained. The amplitude of T(jω) i.e. |T(jω)| is always even function of ω and amplitude response is symmetrical about y-axis.

If ∠ T(jω) = 0 for ω = 0 then the phase response is always an odd function of ω and the phase response is symmetrical about x-axis.

Properties of Open Circuit and Short Circuit Parameters:

The specific properties of z and y parameters can be stated as,

1. The poles of the parameter z₂₁ are also the poles of the parameters z₁₁ and z₂₂. But not all the poles of z₁₁ and z₂₂ are the poles of z₂₁.
2. The poles of the parameter y₂₁ are also the poles of the parameters y₁₁ and y₂₂ , But not all the poles of y₁₁ and y₂₂ are the poles of y₂₁.
3. Let y₁₁, y₂₂ and y₁₂ all have a pole at s = s₁. Let k₁₁ is the residue of y₁₁, k₂₂ is the residue of y₂₂ and k₁₂ is the residue of y₁₁ at the pole s = s₁.

Then for all the two port networks,

This is called a residue condition.