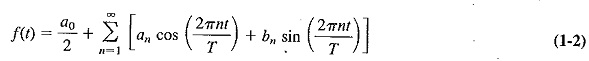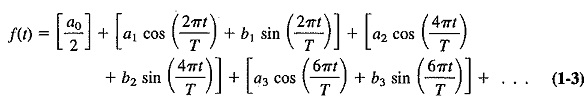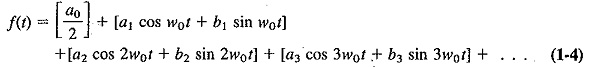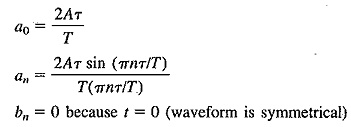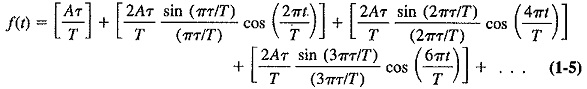Bandwidth Requirement in Communication System:
It is reasonable to expect that the frequency range i.e., Bandwidth Requirement in Communication System for a given transmission should depend on the Bandwidth occupied by the modulation signals themselves. A high-fidelity audio signal requires a range of 50 to 15,000 Hz, but a bandwidth of 300 to 3400 Hz is adequate for a telephone conversation. When a carrier has been similarly modulated with each, a greater bandwidth will be required for the high-fidelity (hi-fi) transmission. At this point, it is worth noting that the transmitted Bandwidth not be exactly the same as the bandwidth of the original signal, for reasons connected with the properties of the modulating systems.
Before trying to estimate the Bandwidth Requirement in Communication System of a modulated transmission, it is essential to know the bandwidth occupied by the modulating signal itself. If this consists of sinusoidal signals, there is no problem, and the occupied bandwidth will simply be the frequency range between the lowest and the highest sine-wave signal. However, if the modulating signals are non sinusoidal, a much more complex situation results. Since such nonsinusoidal waves occur very frequently as modulating signals in communications.
Sine Wave and Fourier Series Formula Review:
It is very important in communications to have a basic understanding of a sine wave signal. Described mathematically in the time domain and in the frequency domain, this signal may be represented as follows:
where
- v(t) = voltage as a function of time
- Em = peak voltage
- sin = trigonometric sine function
- f = frequency in hertz
- ω = radian frequency (ω = 2πf)
- t = time
- Φ = phase angle
If the voltage waveform described by this expression were applied to the vertical input of an oscilloscope, a sine wave would be displayed on the CRT screen.
The symbol f in Equation (1-1) represents the frequency of the sine wave signal. Next we will review the Fourier series, which is used to express periodic time functions in the frequency domain, and the Fourier transform, which is used to express non periodic time domain functions in the frequency domain.
To expand upon the topic of Bandwidth Requirement in Communication System, we will define the terms of the expressions and provide examples so that these topics can be clearly understood.
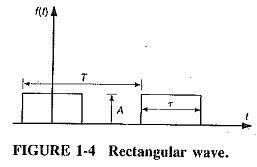
A periodic waveform has amplitude and repeats itself during a specific time period T. Some examples of waveforms are sine, square, rectangular, triangular, and sawtooth. Figure 1-4 is an example of a rectangular wave, where A designates amplitude, T represents time, and τ indicates pulse width. This simplified review of the Fourier series is meant to reacquaint the student with the basics.
The form for the Fourier series is as follows:
Each term is a simple mathematical symbol and shall be explained as follows:
The expression will become clearer when the first four terms are illustrated:
If we substitute ω0 for 2π∕T(ω0=2πf0=2π∕T) in Equation (1-4), we can rewrite the Fourier series in radian terms:
Equation (1-4) supports the statement The makeup of a square or rectangular wave is the sum of (harmonics) the sine wave components at various amplitudes.
The Fourier coefficients for the rectangular waveform in Figure 1-4 are:
The first four terms of this series for the rectangular waveform are:
Frequency Spectra of Non Sinusoidal Wave:
If any nonsinusoidal waves, such as square waves, are to be transmitted by a communications system, then it is important to realize that each such wave may be broken down into its component sine waves. Bandwidth Requirement in Communication System will therefore he considerably greater than might have been expected if only the repetition rate of such a wave had been taken into account.
It may be shown that any nonsinusoidal, single-valued repetitive waveform consists of sine waves and/or cosine waves. The frequency of the lowest-frequency, or fundamental, sine wave is equal to the repetition rate of the nonsinusoidal waveform, and all others are harmonics of the fundamental. There are an infinite number of such harmonics. Some non-sine wave recurring at a rate of 200 times per second will consist of a 200-Hz fundamental sine wave, and harmonics at 400, 600 and 800 Hz, and so on. For some waveforms only the even (or perhaps only the odd) harmonics will be present. As a general rule, it may be added that the higher the harmonic, the lower its energy level, so that in bandwidth calculations the highest harmonics are often ignored.
The preceding statement may be verified in any one of three different ways. It may be proved mathematically by Fourier analysis; Graphical synthesis may be used. In this case adding the appropriate sine-wave components, taken from a formula derived by Fourier analysis, demonstrates the truth of the statement. An added advantage of this method is that it makes it possible for us to see the effect on the overall waveform because of the absence of some of the components (for instance, the higher harmonics).
Finally, the presence of the component sine waves in the correct proportions may be demonstrated with a wave analyzer, which is basically a high-gain tunable amplifier with a narrow bandpass, enabling it to tune to each component sine wave and measure its amplitude. Some formulas for frequently encountered nonsinusoidal waves are now given, and more may be found in handbooks. If the amplitude of the nonsinusoidal wave is A and its repetition rate is ω∕2π per second, then it may be represented as follows:
Square wave:
Triangular wave:
Sawtooth wave:
In each case several of the harmonics will be required, in addition to the fundamental frequency, if the wave is to be represented adequately, (i.e., with acceptably low distortion). This, of course, will greatly increase the Bandwidth Requirement in Communication System.