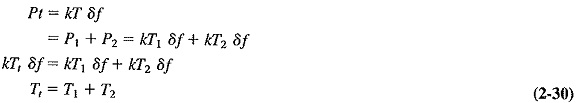Noise Temperature in Communication System:
The concept of noise figure, although frequently used, is not always the most convenient measure of noise, particularly in dealing with UHF and microwave low-noise antennas, receivers or devices. Controversy exists regarding which is the better all-around measurement, but noise Noise Temperature in Communication System, derived from early work in radio astronomy, is employed extensively for antennas and low-noise microwave amplifiers. Not the least reason for its use is convenience, in that it is an additive like noise power. This may be seen from reexamining Equation (2-1), as follows:
where
P1 and P2 = two individual noise powers (e.g., received by the antenna and generated by the antenna, respectively) and Pt is their sum
T1 and T2 = the individual noise temperatures
Tt = the “total” noise temperature
Another advantage of the use of noise temperature for low noise levels is that it shows a greater variation for any given noise-level change than does the noise figure, so changes are easier to grasp in their true perspective.
It will be recalled that the equivalent noise resistance introduced in Section 2-3 is quite fictitious, but it is often employed because of its convenience.
Similarly, Teq, the equivalent Noise Temperature in Communication System, may also be utilized if it proves convenient. In defining the equivalent noise temperature of a receiver or amplifier, it is assumed that R′eq = Ra. If this is to lead to the correct value of noise output power, then obviously R′eq must be at a temperature other than the standard one at which all the components (including Ra) are assumed to be. It is then possible to use Equation (2-24) to equate noise figure and equivalent noise temperature, as follows:
where
R′eq = Ra, as postulated in the definition of Teq
T0 = 17°C = 290 K
Teq = equivalent noise temperature of the amplifier or receiver whose noise figure is F
Note that F here is a ratio and is not expressed in decibels. Also, Teq may be influenced by (but is certainly not equal to) the actual ambient temperature of the receiver or amplifier. It must be repeated that the equivalent noise temperature is just a convenient fiction. If all the noise of the receiver were generated by Ra, its temperature would have to be Teq. Finally we have, from Equation (2-31),
Once noise figure is known, equivalent noise temperature may be calculated from Equation (2-32), or a nomograph may be constructed if use is frequent enough to justify it. Graphs of Noise Temperature in Communication System of various sources versus frequency and sky temperature versus frequency are also available.