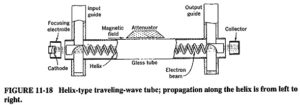
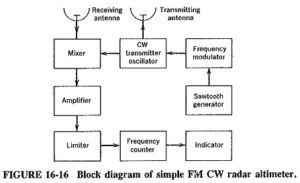
Internal Noise in Communication System:
Under the heading of Internal Noise in Communication System, we discuss noise created by any of the active or passive devices found in receivers. Such noise is generally random, impossible to treat on an individual voltage basis, but easy to observe and describe statistically. Because the noise is randomly distributed over the entire radio spectrum there is, on the average, as much of it at one frequency as at any other.
“Random noise power is proportional to the bandwidth over which it is measured.”
Thermal Agitation Noise:
The noise generated in a resistance or the resistive component is random and is referred to as thermal, agitation, white or Johnson noise. It is due to the rapid and random motion of the molecules (atoms and electrons) inside the component itself.
In thermodynamics, kinetic theory shows that the ‘temperature of a particle is a way of expressing its internal kinetic energy. Thus the “temperature” of a body is the statistical root mean square (rms) value of the velocity of motion of the particles in the body. As the theory states, the kinetic energy of these particles becomes approximately zero (i.e., their motion ceases) at the temperature of absolute zero, which is 0 K (kelvins, formerly called degrees Kelvin) and very nearly equals -273°C. It becomes apparent that the noise generated by a resistor is proportional to its absolute temperature, in addition to being proportional to the bandwidth over which the Internal Noise in Communication System is to be measured. Therefore.
where
k = Boltzmann’s constant = 1.38 x 10-23 J(joules)/K the appropriate proportionality constant in this case
T = absolute temperature, K = 273 + °C
δf = bandwidth of interest
Pn = maximum noise power output of a resistor
α = varies directly
If an ordinary resistor at the standard temperature of 17°C (290 K) is not connected to any voltage source, it might at first be thought that there is no voltage to be measured across it. That is correct if the measuring instrument is a direct current (dc) voltmeter, but it is incorrect if a very sensitive electronic voltmeter is used. The resistor is a noise generator, and there may even be quite a large voltage across it. Since it is random and therefore has a finite rms value but no dc component, only the alternating current (ac) meter will register a reading. This Internal Noise in Communication System voltage is caused by the random movement of electrons within the resistor, which constitutes a current. It is true that as many electrons arrive at one end of the resistor as at the other over any long period of time. At any instant of time, there are bound to be more electrons arriving at one particular end than at the other because their movement is random. The rate of arrival of electrons at either end of the resistor therefore varies randomly, and so does the potential difference between the two ends. A random voltage across the resistor definitely exists and may be both measured and calculated.
It must be realized that all formulas referring to random noise are applicable only to the rms value of such noise, not to its instantaneous value, which is quite unpredictable. So far as peak noise voltages are concerned, all that may be stated is that they are unlikely to have values in excess of 10 times the rms value.
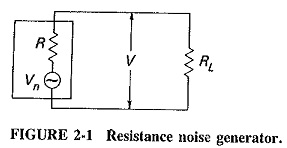
Using Equation (2-1), the equivalent circuit of a resistor as a noise generator may be drawn as in Figure 2-1, and from this the resistor’s equivalent noise voltage Vn may be calculated. Assume that RL is noiseless and is receiving the maximum noise power generated by R; under these conditions of maximum power transfer, RL must be equal to R. Then
It is seen from Equation (2-2) that the square of the rms noise voltage associated with a resistor is proportional to the absolute temperature of the resistor, the value of its resistance, and the bandwidth over which the noise is measured. Note especially that the generated noise voltage is quite independent of the frequency at which it is measured. This stems from the fact that it is random and therefore evenly distributed over the frequency spectrum.
Shot Noise:
Thermal agitation is by no means the only source of noise in receivers. The most important of all the other sources is the shot effect, which leads to shot noise in all amplifying devices and virtually all active devices. It is caused by random variations in the arrival of electrons (or holes) at the output electrode of an amplifying device and appears as a randomly varying noise current superimposed on the output. When amplified, it is supposed to sound as though a shower of lead shot were falling on a metal sheet. Hence the name shot noise.
Although the average output current of a device is governed by the various bias voltages, at any instant of time there may be more or fewer electrons arriving at the output electrode. In bipolar transistors, this is mainly a result of the random drift of the discrete current carriers across the junctions. The paths taken are random and therefore unequal, so that although the average collector current is constant, minute variations nevertheless occur. Shot noise behaves in a similar manner to thermal agitation Internal Noise in Communication System, apart from the fact that it has a different source.
Many variables are involved in the generation of this noise in the various amplifying devices, and so it is customary to use approximate equations for it. In addition, shot-noise current is a little difficult to add to thermal-noise voltage in calculations, so that for all devices with the exception of the diode, shot-noise formulas used are generally simplified. For a diode, the formula is exactly
where
in = rms shot-noise current
e = charge of an electron = 1.6 X 10-19C
ip = direct diode current
δf = bandwidth of system
Note: It may be shown that, for a vacuum tube diode, Equation (2-3) applies only under so-called temperature-limited conditions, under which the “virtual cathode” has not been formed.
In all other instances not only is the formula simplified but it is not even a formula for shot-noise current. The most convenient method of dealing with shot noise is to find the value or formula for an equivalent input-noise resistor. This precedes the device, which is now assumed to be noiseless, and has a value such that the same amount of noise is present at the output of the equivalent system as in the practical amplifier. The noise current has been replaced by a resistance so that it is now easier to add shot noise to thermal noise. It has also been referred to the input of the amplifier, which is a much more convenient place, as will be seen.
The value of the equivalent shot-noise resistance Reg of a device is generally quoted in the manufacturer’s specifications. Approximate formulas for equivalent shot-noise resistances are also available. They all show that such noise is inversely proportional to transconductance and also directly proportional to output current. So far as the use of Reg is concerned, the important thing to realize is that it is a completely fictitious resistance, whose sole function is to simplify calculations involving shot noise. For Internal Noise in Communication System only, this resistance is treated as though it were an ordinary noise-creating resistor, at the same temperature as all the other resistors, and located in series with the input electrode of the device.
Transit-Time Noise:
If the time taken by an electron to travel from the emitter to the collector of a transistor becomes significant to the period of the signal being amplified, i.e., at frequencies in the upper VHF range and beyond, the so-called transit-time effect takes place, and the noise input admittance of the transistor increases. The minute currents induced in the input of the device by random fluctuations in the output current become of great importance at such frequencies and create random noise (frequency distortion).
Once this high-frequency noise makes its presence felt, it goes on increasing with frequency at a rate that soon approaches 6 decibels (6 dB) per octave, and this random noise then quickly predominates over the other forms. The result of all this is that it is preferable to measure noise at such high frequencies, instead of trying to calculate an input equivalent noise resistance for it. Radio frequency (RF) transistors are remarkably low-noise. A noise figure (see Section 2-4) as low as 1 dB is possible with transistor amplifiers well into the UHF range.
Miscellaneous Noise:
Flicker:
At low audio frequencies, a poorly understood form of noise called flicker or modulation noise is found in transistors. It is proportional to emitter current and junction temperature, but since it is inversely proportional to frequency, it may be completely ignored above about 500 Hz. It is no longer very serious.
Resistance:
Thermal noise, sometimes called resistance noise, it also present in transistors. It is due to the base, emitter, and collector internal resistances, and in most circumstances the base resistance makes the largest contribution.
From above 500 Hz up to about fαb/5, transistor noise remains relatively constant, so that an equivalent input resistance for shot and thermal noise may be freely used.
Noise in mixers:
Mixers (nonlinear amplifying circuits) are much noisier than amplifiers using identical devices, except at microwave frequencies, where the situation is rather complex. This high value of noise in mixers is caused by two separate effects. First, conversion transconductance of mixers is much lower than the transconductance of amplifiers. Second, if image frequency rejection is inadequate, as often happens at shortwave frequencies,Internal Noise in Communication System associated with the image frequency will also be accepted.