Energy Band Theory of Crystals:
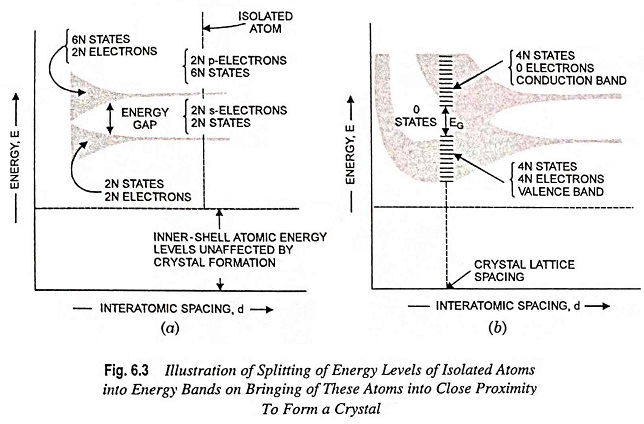
Energy Band Theory of Crystals – As discussed above, it is revealed that most metals and semiconductors are crystalline in structure and a crystal is made up of a space array of atoms or molecules (strictly speaking, ions) in regular repetition in three dimensions of some fundamental structural unit. For a gaseous element, the electronic energy levels are the same as for a single free atom because the individual atoms in a gas are well apart and has negligible influence on each other. However, in a crystal the individual atoms are so closely packed that the resulting energy levels are modified because of interaction between the atoms. When atoms form crystal, the energy levels of the inner-shell electrons are not appreciably affected. However, the energy levels of the outer-shell electrons are altered considerably as these electrons are shared by adjacent atoms in the crystal. It has been found that coupling between the outer-shell electrons of the atoms results in a band of closely spaced energy states instead of the widely separated energy levels of the isolated atom, as shown in Fig. 6.3.
For understanding the formation of Energy Band Theory of Crystals, let us consider a silicon crystal made up of N atoms and assume that there is a possibility of varying the spacing between atoms without affecting the type of fundamental crystal structure. If the atoms are so distant apart that there is negligible interaction between them, the energy levels will coincide with those of the isolated atom. As already mentioned in Art. 6.2, the outer two subshells for each element indicated in Table 6.1 have two s electrons and two p electrons.
Thus if the inner-shell levels are ignored, then, as shown to the extreme right in Fig. 6.3 (a), there are 2N electrons completely filling the 2N possible s levels, all at the same energy. Since the p-atomic subshells have 6 possible states, our imaginary crystal of widely spaced atoms has 2N electrons, which fill only one-third of the 6N possible p states, all at the same energy level.
If the interatomic spacing is gradually reduced, i.e., moving from right to left in Fig. 6.3 (a), there will be a gradual increase in the interaction between the neighboring atoms. Because of this interaction, the atomic-wave functions overlap and the crystal becomes an electronic system which must obey the Pauli exclusion principle. Thus the 2N s states spread out to form a band of energy. The separation between energy levels is small, but since N is very large (of the order of 1023 cm-3), the total spread between the minimum and maximum energy levels becomes large. This spread will have several eV of energy and is referred to as energy band, and is depicted schematically by the lower shaded region in Fig. 6.3 (a). The 2N states in this band are completely filled with 2N electrons. In the same way, the upper shaded region in Fig. 6.3 (a) is a band of 6N states which has only 2N of its levels occupied by the electrons (4N states remain unoccupied).
An energy gap exists between the two energy bands. This energy gap is known as forbidden energy gap, as no electrons can occupy states in this gap. This forbidden energy gap decreases as the atomic spacing is reduced and becomes zero with further reduction in the interatomic spacing, as shown in Fig. 6.3 (b). Under such circumstances the 6N upper states merge with the 2N lower states, providing a total of 8N levels, half of which are occupied by the 2N + 2N = 4N available electrons. These 4N electrons now no longer belong to either p subshell or s subshells of an isolated atom but belong to the crystal as a whole. Thus, at this interatomic spacing, each atom in the crystal can contribute 4 electrons to the crystal. The band occupied by these contributed electrons is known as the valence band.
If the spacing between atoms is reduced below the distance at which the bands overlap, the interaction between atoms becomes extremely large, and the Energy Band Theory of Crystals structure assumes the shape depicted in Fig. 6.3 (b). The exact Energy Band Theory of Crystals structure depends upon (i) the orientation of the atoms relative to one another in space (i.e., the crystal structure) and upon the atomic number, that determines the electrical constitution of each atom. At the crystal-lattice spacing (the dashed vertical line) we find the valence band filled with 4N electrons separated by a forbidden band of extent EG from the empty band consisting of 4N additional states. The upper vacant band is known as the conduction band.