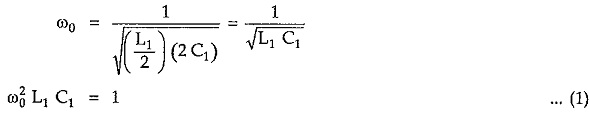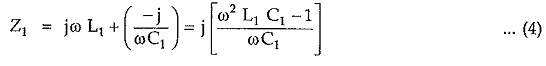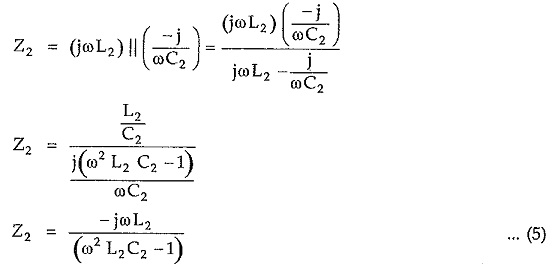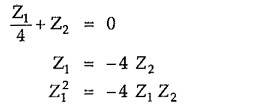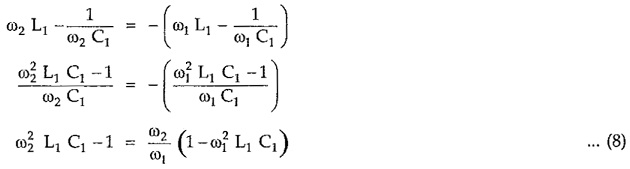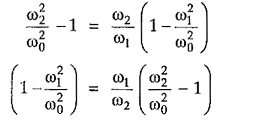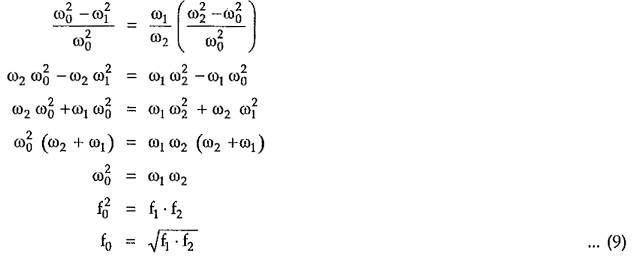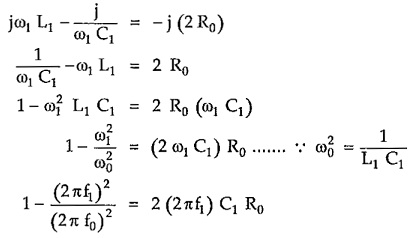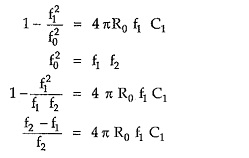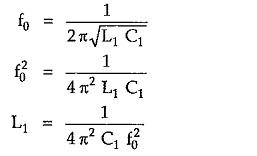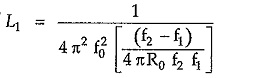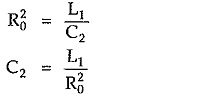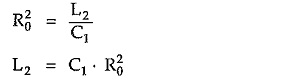Band Pass Filter

Band Pass Filter:

Band pass filter pass a certain range of frequencies (called as pass band) while attenuate all other frequencies. Such band pass filters can be obtained by connecting low pass filter sections in cascade with high pass filter sections as shown in Fig. 9.15.

In above type of connection, the cut-off frequency of low pass filter section must be selected higher than that of high pass filter section.

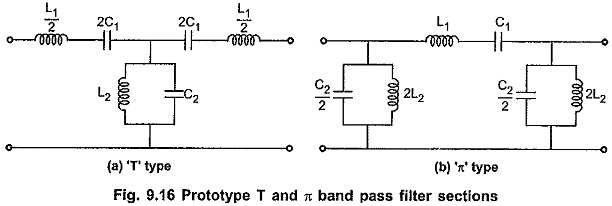
Although cascade connection of low pass filter and high pass filter sections functions properly as band pass filter, it is more economical to combine both sections in one single filter section. An alternative form of band pass filter can be obtained either as a T or π section if series arm contains a series resonant circuit while the shunt arm contains a parallel resonant circuit as shown in the Fig. 9.16 (a) and (b).

The band pass filter characteristics can be obtained by using conventional band pass filter (either T or π type) as shown in the Fig. 9.16, if the series resonant frequency of the series arm is selected same as anti resonant frequency of the shunt arm. Consider T type band pass filter section as shown in the Fig. 9.16 (a). Let the frequency of series and shunt arm be ω₀ rad/sec.

Then, for series arm, frequency of resonance is given by,

Similarly for shunt arm, frequency of anti resonance is given by,

From equations (1) and (2), for same resonant frequencies of series and shunt arms we can write,

Design Impedance (R₀):

Total series arm impedance Z₁ is given by

Similarly, total shunt arm impedance Z₂ is given by

Hence, Z₁ Z₂ = L₂/C₁ = L₁/C₂which is real and constant. Hence above sections are constant k sections. So we can write,

Reactance Curves and Expressions for Cut-off Frequencies:

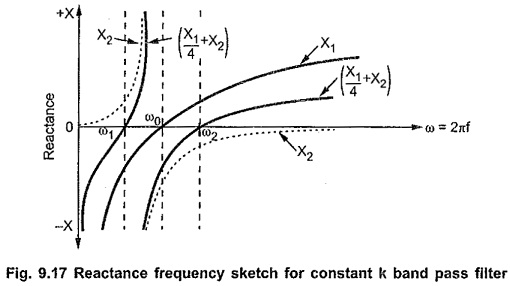
To verify the band pass characteristics, let Z₁ = j X₁ and Z₂ =j X₂. Similar to the reactance curves drawn for low pass filter section and high pass filter section, sketching reactances X₁ and (X₁/4 + X₂) against frequency f as shown in the Fig. 9.17.

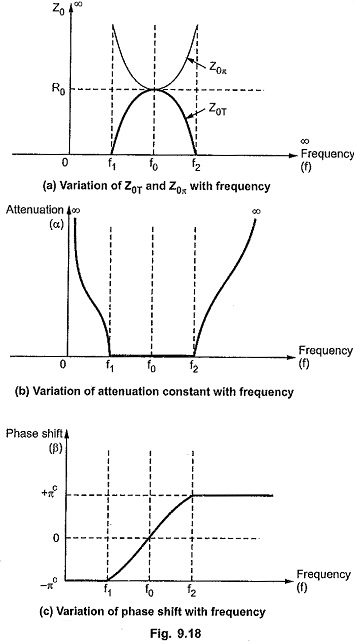
From the above characteristics it is clear that the reactance curves for X₁ and (X₁/4 + X₂) are on the same sides the axis below f₁ and above f₂. At the same time, the reactance curves between f₁ and f₂ are on opposite sides of frequency axis. Thus frequencies between f₁ and f₂ constitute a pass band ; while the frequencies below f₁ and above f₂ give stop band. Hence the section considered shows band pass filter characteristics where f₁ and f₂ are lower and upper cut-off frequencies of the filter.

In band pass filter, condition for cut-off frequency is,

But from the condition of constant-k filter section, Z₁ Z₂ = R²₀

From above equation (7) it is clear that the value of the series arm impedance Z₁ can be obtained at two different cut-off frequencies namely f₁ and f₂. So at f = f₁, Z₁ = – j(2 R₀) and at f = f₂ , Z₁ = + j(2 R₀). Thus impedance Z₁ at f₁, i.e. lower cut-off frequency, is negative of the impedance Z₁ at f₂ i.e. upper cut-off frequency. Hence we can write,

But from equation (1) we can write,

Substituting value of (L₁ C₁) in above equation (8), we can write,

Simplifying above equation,

Hence, above equation (9) indicates that frequency of resonance of the individual arms is the geometric mean of two cut-off frequencies:

Variation of Z_0T and Z_0π, Attenuation Constant (α) and Phase Constant (β) with Frequency:

The variations of Z_0T and Z_0π, attenuation constant (α) and phase shift (β) with frequency are as shown in the Fig. 9.18. (a), (b) and (c). Consider that the design impedance of band pass filter is R₀ and cut-off frequencies are f₁ and f₂.