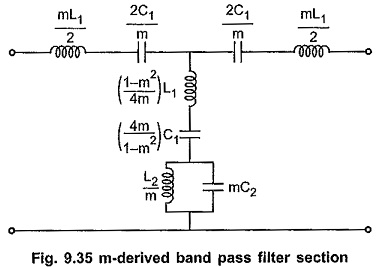
m Derived Band Pass Filter:
We can obtain m Derived Band Pass Filter if the prototype band pass filter is simplified according to the network in the Fig. 9.35 which has been used to obtain m-derived low pass and high pass sections.
The T section in each case will have a shunt impedance, Z2/m + (1-m2/4m) Z1 where Z1 and Z2 are the impedances of the prototype sections. We can get m-derived band pass section if we substitute values of Z1 and Z2 of prototype band pass filter section in equation,
The m Derived Band Pass Filter section is as shown in the Fig. 9.35.
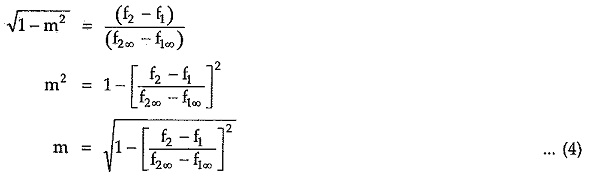
If we substitute Z1 and Z2 in equation (1), we can get two values of frequencies. These frequencies are frequencies of infinite attenuation namely f1∞ and f2∞. If the frequency of resonance is f0, then the relationship between cut-off frequencies, and frequencies of infinite attenuation is given by,
Also we can write
Simplifying above equation,
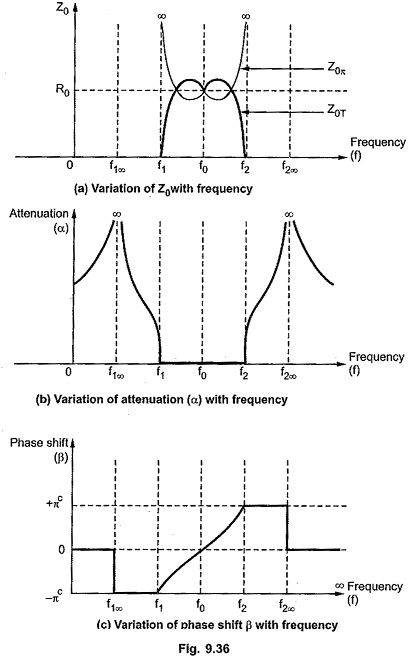
Variations of Characteristic Impedance (Z0) Attenuation Constant (α) and Phase Shift (β) with Frequency:
The variations of characteristic impedance (Z0), attenuation constant (α) and phase shift (β) with frequency are as shown in the Fig. 9.36 (a), (b) and (c).