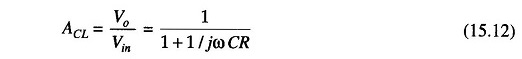Low Pass Filter Circuits:

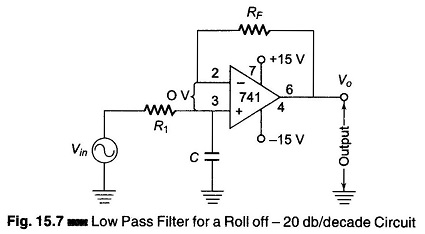
The Low Pass Filter Circuits of Fig. 15.7 is commonly used for low pass active filters. The filtering is done by the use of an RC network. The opamp is used as a unity gain amplifier. The resistor R_F is equal to R₁.

(At dc, the capacitive reactance is infinite and the dc resistance path to ground for both input terminals must be equal.) The difference voltage between inverting and non-inverting inputs is essentially O V. Hence, the voltage across the capacitor C equals the output voltage. Since this circuit is a voltage follower, V_in divides between R and C. The capacitor voltage V_o is given by

where ω is the frequency of V_in in radians per second (ω = 2 πf and j is the imaginary term. To obtain the closed loop voltage gain A_CL, we have,

Consider the Eq. (15.12). At very low frequencies, as ω approaches 0, | A_CL | = 1, and at very high frequencies, as ω approaches infinity, | A_CL | = 0. Hence this filter is a Low Pass Filter Circuits.

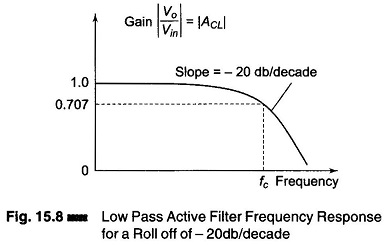
Figure 15.8 shows a frequency response of ω versus | A_CL |. For frequencies greater than the cutoff frequency ω_c, | A_CL | decreases at a rate of 20 db/decade. This is the same as saying that the voltage gain is divided by 10 when the frequency of ω is increased by 10.

The cutoff frequency is defined as that frequency of V_in where | A_CL | is reduced to 0.707 times its low frequency value. The cutoff frequency is calculated from

Therefore,

Where

• f_c = is the cutoff frequency in Hz
• R = resistance in Ω
• C = capacitance in Farad.

The Eq. (15.13) can be rearranged to solve R, ignore to give