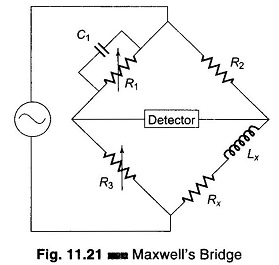
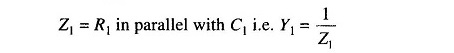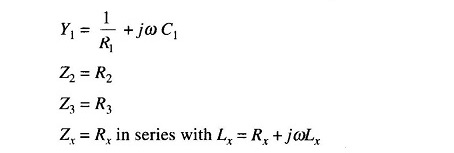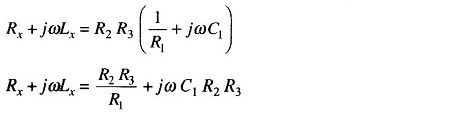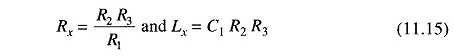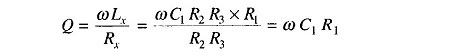Maxwell Bridge Theory:
Maxwell Bridge theory, shown in Fig. 11.21, measures an unknown inductance in terms of a known capacitor. The use of standard arm offers the advantage of compactness and easy shielding. The capacitor is almost a loss-less component. One arm has a resistance R1 in parallel with C1, and hence it is easier to write the balance equation using the admittance of arm 1 instead of the impedance.
The general equation for bridge balance is
i.e.
where
From Eq. (11.14) we have
Equating real terms and imaginary terms we have
Also
Maxwell Bridge Theory is limited to the measurement of low Q values (1 – 10). The measurement is independent of the excitation frequency. The scale of the resistance can be calibrated to read inductance directly.
Advantages and Disadvantages:
The Maxwell bridge using a fixed capacitor has the disadvantage that there is an interaction between the resistance and reactance balances. This can be avoided by varying the capacitances, instead of R2 and R3, to obtain a reactance balance. However, the bridge can be made to read directly in Q.
The bridge is particularly suited for inductances measurements, since comparison with a capacitor is more ideal than with another inductance. Commercial bridges measure from 1 – 1000 H, with ± 2% error. (If the Q is very large, R1 becomes excessively large and it is impractical to obtain a satisfactory variable standard resistance in the range of values required).