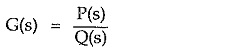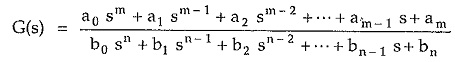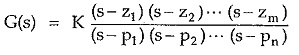Poles and Zeros of Network Function:

All the Poles and Zeros of Network Function have the form of a ratio of two polynomials in s as,

The P(s) is the numerator polynomial in s having degree m while the Q(s) is the denominator polynomial in s having degree n. Hence network function can be expressed as,

Now the equation P(s) = 0 has m roots while the equation Q(s) = 0 has n roots. Thus G(s) can be expressed in the factorized form as,

where z₁, z₂, … z_m are the roots of the equation P(s) = 0 and P₁, P₂, … P_n are the roots of the equation Q(s) = 0.

The z₁, z₂, … z_m,P₁,P₂ … P_n are the values of s and hence are complex frequencies as s variable is a complex variable.

Poles:

The values of ‘s’ i.e. complex frequencies, which make the network function infinite when substituted in the denominator of a network function are called poles of the network function.

If such poles are real and nonrepeated, these are called simple poles. If a particular pole has same value twice or more than that, it is called repeated pole. A pair of poles with complex conjugate values is called a pair of complex conjugate poles.

The poles are the roots of the equation obtained by equating denominator polynomial of a network function to zero. Such an equation is called characteristic equation of a network.

Zeros:

The values of ‘s’ i.e. complex frequencies, which make the network function zero when substituted in the numerator of a network function are called zeros of the network function.

Similar to the poles, zeros also can be simple zeros, repeated zeros or complex conjugate zeros.

The zeros are the roots of the equation obtained by equating numerator polynomial of a system function to zero.

When the order m is greater than n then there are m-n poles at infinity while if the order m is less than n then there are n-m zeros at infinity. Hence if, for any rational network function, poles and zeros at infinity and zero are taken into consideration in addition to finite poles and zeros, the total number of zeros is equal to the total number of poles.

D.C. Gain of the Network:

The s variable is a complex frequency variable given by s = jω in the frequency domain. The frequency of d.c. is zero hence value of G(s) calculated at ω = 0 i.e. s = 0 is called d.c. gain of the network, represented by the network function G(s). For s = 0, the value of G(s) is constant representing gain of the network at zero frequency.