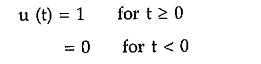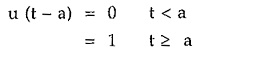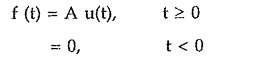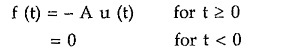Laplace Transform of Unit Step Function:

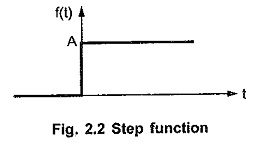
The step function is shown in the Fig. 2.2.

Such a function has zero value for all t < 0, while has a value A for t ≥ 0.

Hence mathematically it is expressed as,

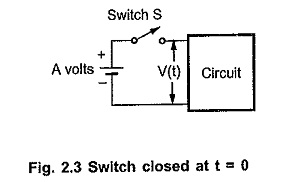
where A is called magnitude of the step. In network analysis, the step function is analogous to the switch which closes at t = 0 and connects a d.c. battery of A volts to the given circuit as shown in the Fig. 2.3. Note that the step voltage to the circuit gets applied whenever the switch S gets closed.

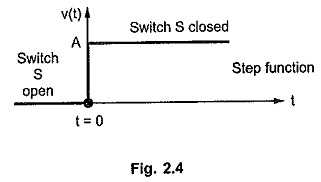
The waveform of step function V(t) for the circuit is shown in the Fig. 2.4.

Unit Step Function [u(t)]:

Whenever the magnitude of the step is unity i.e. A = 1, the step function is called unit step functions. Whenever the argument within bracket i.e. (t) is negative, the unit step functions u(t) is zero.

Thus mathematically it can be defined as,

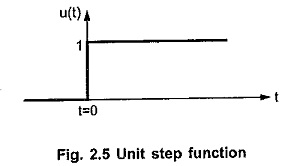
The waveform of unit step functions is shown in the Fig. 2.5.

Shifted Unit Step Functions:

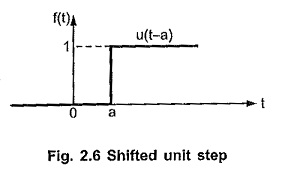
The time at which the step occurs need not be always zero, it may be other than zero. Now as per the basic feature of unit step functions, whenever the argument within bracket is negative, the function value is zero while it is unity when the argument within bracket is positive. Thus if the step occurs at t = a rather than at t = 0, mathematically it is expressed as,

For t < a, the argument in bracket i.e. (t – a) is negative hence the function is zero. Such a function is shown in the Fig. 2.6. Thus the shift to the right hand side towards positive values of t is denoted by argument (t – a) in the bracket. Such a function is also called delayed function.

Use of Unit Step Function:

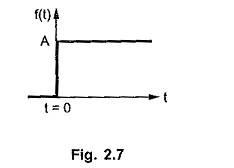
The unit step functions is useful to express the positive and negative magnitude step functions. Consider the positive magnitude step function shown in the Fig. 2.7.

Such a function can be expressed using unit step functions as,

This indicates that f(t) is multiplied by unit step functions u(t). And as u(t) has unit magnitude, it does not affect the value of the original function.

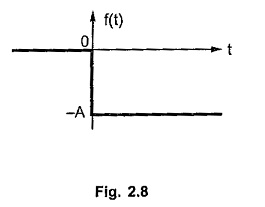
Consider the step function with negative amplitude of -A as shown in the Fig. 2.8.

Such a function can be expressed using u(t) as,

So the multiplication of a function by u(t) clearly indicates that the function does not exist before t = 0.