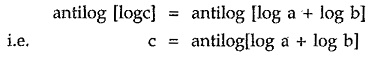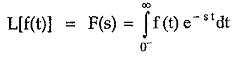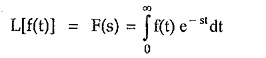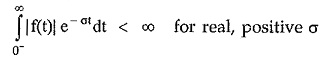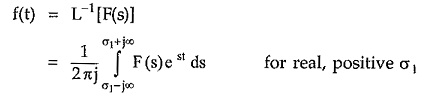Definition of Laplace Transform:
Here we are going to discuss one of such transform methods called Laplace Transform Method which transforms the time domain differential equations to the frequency domain. To understand the philosophy of transform method, let us see the analogy between transform method and the use of logarithms for arithmetic operations.
Consider the two real numbers a and b, which are to be multiplied. The product is say c.
Taking logarithm of both sides we get,
Taking inverse logarithm i.e. anti-log of both sides,
What is the advantage of using logarithmic method? The product gets converted to a sum. So if the numbers a and b are too big like six digits or more, the logarithmic method makes it easy to add the logarithms of a and b rather than multiplying them directly. Finally taking inverse logarithm of the addition, the product c can be obtained.
Exactly same is the philosophy of the Laplace transforms method. Consider a differential equation,
where f(t) is the input forcing function, x(t) is unknown say current or voltage interms of network analysis while y[x(t)] represents a differential equation. Taking Laplace transforms of both sides, the differential equation gets converted to an algebraic equation interms of a frequency variable denoted as ‘s’.
where X(s) is transform of x(t), F(s) is transform of f(t) and Y(X(s),s) is the algebraic equation in s.
Thus Laplace transform converts integro-differential time domain equations into simple algebraic frequency domain equations interms of a variables ‘s’. Now it becomes very easy to perform algebraic operations to obtain the expression for X(s). Finally taking inverse Laplace transforms of X(s), the solution x(t) in the time domain can be obtained.
where T–1 indicates inverse transform of X(s) which is similar to the operation of taking inverse logarithm i.e. antilog, as seen earlier. The table of Laplace transform pairs {x(t), X(s)} is available, which further simplifies the job of finding Laplace transforms as well as inverse Laplace transforms.
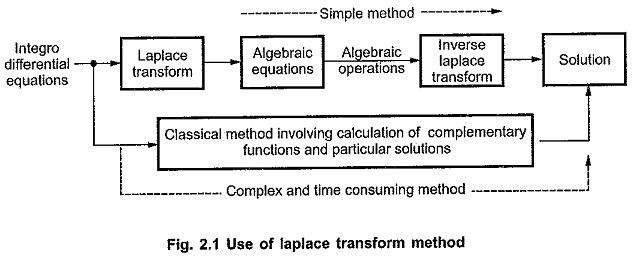
The Laplace transform method provides very simple way of solving the complicated integro-differential time domain equations, by converting them into simple algebraic equations in the frequency domain. This is the essence of the Laplace transform method. The Fig. 2.1 shows the philosophy of the Laplace transform method.
Definition:
Let us define the Laplace transform of a time domain function.
If f(t) is the time domain function then its Laplace transforms is denoted by F(s) and is defined by the equation,
where s is the complex frequency variable and is given by,
The real part σ is called attenuation constant or damping factor while ω which is the imaginary part of s is the angular frequency.
To take into account the possibility that f(t) may be an impulse or one of its higher derivatives, the lower limit of integration is taken as 0–. This includes the time just before the instant t = 0.
In the case when no impulses or higher order derivatives of impulses are involved i.e. for continuous functions f(0–) = f(0+), then for such functions, the integration can be effectively taken from zero to infinity.
The given function f(t) possesses a Laplace transforms only if it satisfies the condition given by,
Similar to the Laplace transform, the inverse Laplace transform giving time domain function from frequency domain is defined as,
The definition of inverse Laplace transform includes the complex integration. The calculation using complex integration is much more complicated hence the method of partial fraction expansion is generally used to calculate the inverse Laplace transforms.