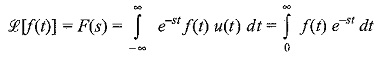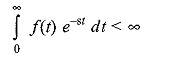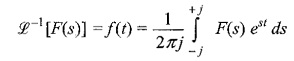Definition of Laplace Transform:

The Definition of Laplace Transform is used to solve differential equations and corresponding initial and final value problems. Laplace transforms are widely used in engineering, particularly when the driving function has discontinuities and appears for a short period only.

In circuit analysis, the input and output functions do not exist forever in time. For casual functions, the function can be defined as f(t) u(t). The integral for the Laplace transform is taken with the lower limit at t = 0 in order to include the effect of any discontinuity at t = 0.

Consider a function f(t) which is to be continuous and defined for values of t ≥ 0. The Definition of Laplace Transform is then

f(t) is a continuous function for t ≥ 0 multiplied by e^-st which is integrated with respect to t between the limits 0 and ∞. The resultant function of the variables is called Laplace transform of f(t).

Laplace transform is a function of independent variable s corresponding to the complex variable in the exponent of e^-st. The complex variable s is, in general, of the form S = σ + jω and σ and ω being the real and imaginary parts, respectively. For a function to have a Laplace transform, it must satisfy the condition

Laplace transform changes the time domain function f(t) to the frequency domain function F(s). Similarly, inverse Laplace transformation converts frequency domain function F(s) to the time domain function f(t) as shown below.

Here, the inverse transform involves a complex integration. f(t) can be represented as a weighted integral of complex exponentials. We will denote the transform relationship between f(t) and F(s) as