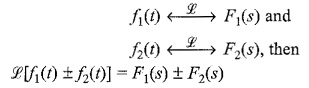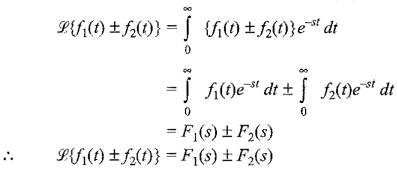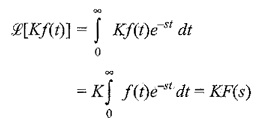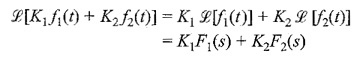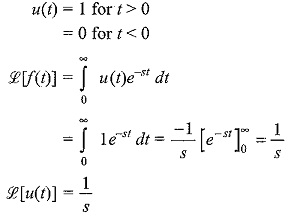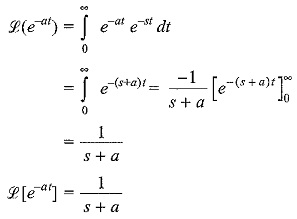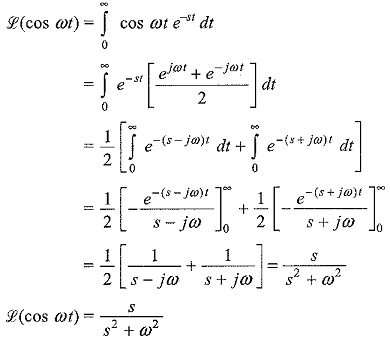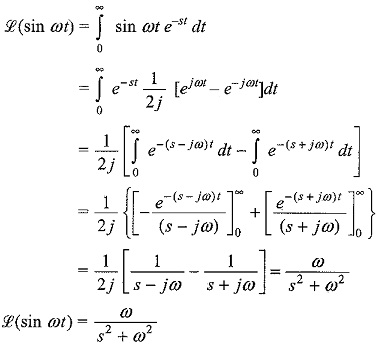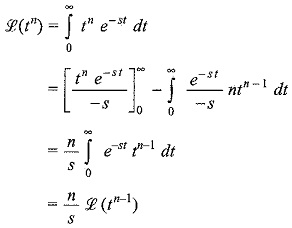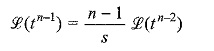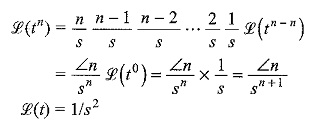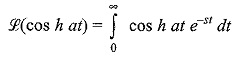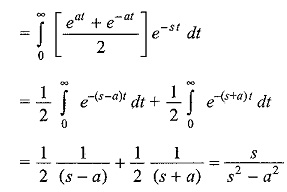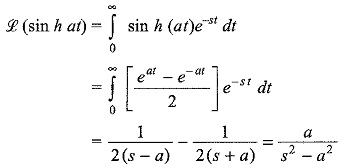Laplace Properties:

Laplace transforms have the following Laplace Properties.

(a) Superposition Property:

The first Laplace Properties is Superposition Property. The Laplace transform of the sum of the two or more functions is equal to the sum of transforms of the individual function,

i.e. if

Consider two functions f₁(t) and f₂(t). The Laplace transform of the sum or difference of these two functions is given by

(b)Linearity property:

The first Laplace Properties is Linearity Property. If K is a constant, then

Consider a function f(t) multiplied by a constant K. The Laplace transform of this function is given by

If we can use these two properties jointly, we have

Laplace Transform of Some Useful Functions:

(i) The unit step function f(t) = u(t)

where

(ii) Exponential function f(t) = e^-at

(iii) The cosine function: cos ωt

(iv) The sine function: sin ωt

(v) The function tⁿ, where n is a positive integer

Similarly,

By taking Laplace transformations of t^n-2, t^n-3,…. and substituting in the above equation, we get

(vi) The hyperbolic sine and cosine function

Similarly,