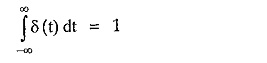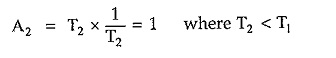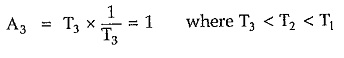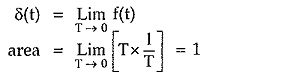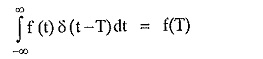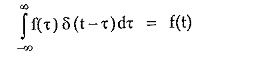Laplace Transform of Impulse Function:

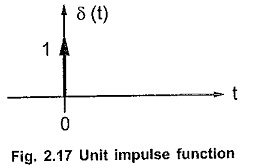
The Laplace Transform of Impulse Function is a function which exists only at t = 0 and is zero, elsewhere. The impulse function is also called delta function. The unit impulse function is denoted as δ(t). The amplitude of impulse function is infinitely large at t = 0, but for unit impulse function the area under the curve is equal to one. The unit impulse function is shown in the Fig. 2.17.

Laplace Transform of Impulse Function

The one, in the Fig. 2.17 near arrow, indicates the area under the pulse.

Mathematically it is represented as, δ(t) = 0 t ≠ 0

and area under the pulse is unity i.e.

The concept of unit impulse function can be further simplified by the following discussion.

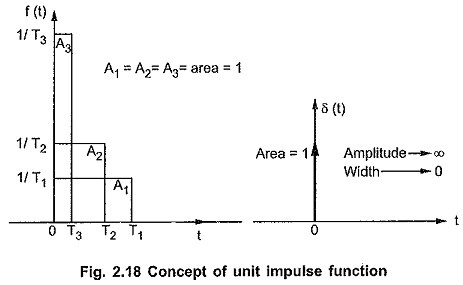
Consider a rectangular pulse of unit area having width T1 and amplitude 1/T1.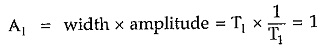Laplace Transform of Impulse Function

If now width is decreased from T1 to T2 then to have unit area of pulse its amplitude must increase from 1/T1 to 1/T2

Laplace Transform of Impulse Function

If the width is further decreased to T3 then to have unit area of pulse its amplitude will further increase to 1/T3.

Laplace Transform of Impulse Function

In the limiting case now if the width tends to zero then the amplitude of the pulse tends to infinity to get the unit area. Such a function i.e. pulse with infinite amplitude and zero width, having unit area under the pulse is called unit impulse function or delta function.

Laplace Transform of Impulse Function

From the Fig. 2.18 we can write that if f(t) is the pulse with width T then the unit impulse function is,

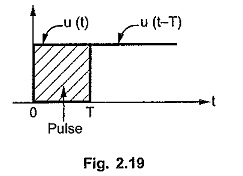
Laplace Transform of Impulse Function

The unit impulse function can also be obtained using step functions. The unit impulse function is the limiting case of a rectangular pulse. A rectangular pulse can be obtained by subtraction of two step functions as shown in the Fig. 2.19.

Hence the rectangular pulse can be expressed as,

this is a pulse of width T.

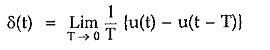
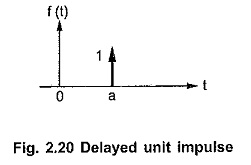
Hence unit impulse function having unit area under pulse can be written as,Laplace Transform of Impulse Function

Delayed Unit Impulse Function:

Similar to the delayed step and ramp, there can exist a delayed unit impulse function.

Laplace Transform of Impulse Function

It has an unit area, but existing at t = a as shown in the Fig. 2.20. It is denoted as,

Important Properties of Impulse Function:

There are two important properties of impulse functions.

Shifting Property :

Mathematically this property is expressed by the integral,

where δ(t — T) is delayed impulse function.

Replication Property :

This property is mathematically given by,

Laplace Transform of Impulse Function

This property tells that the convolution of any function with an impulse function results into the original function.

Related posts:

  1. Laplace Transform of Unit Step Function
  2. Laplace Transform of Periodic Function
  3. Definition of Laplace Transform
  4. Laplace Transform Properties
  5. Laplace Transform of Standard Functions
  6. Inverse Laplace Transform
  7. Definition of Laplace Transform
  8. Laplace Transform Partial Fraction
  9. Application of Laplace Transform
  10. Transfer Function or Network Function
  11. Gate Function in Network Function
  12. Laplace Properties
  13. Laplace Theorem
  14. Standard Impulse Wave Shapes
  15. Circuits for Producing Impulse Waves
  16. Multistage Impulse Generator Circuit
  17. Generation of Impulse Current Generator Output Waveform
  18. Tripping of Impulse Generators
  19. Series Inductance in Impulse Generator Circuit
  20. Finite Impulse Response Filters Interview Questions and Answers