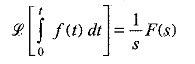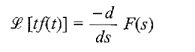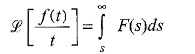Laplace Theorem:

The Laplace theorem is given by

• Differentiation Theorem
• Integration Theorem
• Differentiation of Transforms
• Integration of transforms
• First Shifting Theorem
• Second Shifting Theorem
• Initial Value Theorem
• Final Value Theorem

(a) Differentiation Theorem:

If a function f(t) is piecewise continuous, then the Laplace transform of its derivative d/dt [f(t)] is given by

(b)Integration Theorem:

If a function f(t) is continuous, then the Laplace transform of its integral ∫ f(t)dt is given by

(c) Differentiation of Transforms:

If the Laplace transform of the function f(t) exists, then the derivative of the corresponding transform with respect to s in the frequency domain is equal to its multiplication by t in the time domain.

(d) Integration of transforms:

If the Laplace transform of the function f(t) exists, then the integral of corresponding transform with respect to s in the complex frequency domain is equal to its division by t in the time domain.

(e) First Shifting Theorem:

If the function f(t) has the transform F(s), then the Laplace transform of

e^-at f(t) is F(s + a)

(f) Second Shifting Theorem:

If the function f(t) has the transform F(s), then the Laplace transform of

f(t – a)u (t – a) is e^-as F(s)

(g) Initial Value Theorem:

If the function f(t) and its derivative f′(t) are Laplace transformable then

(h) Final Value Theorem:

The final Laplace Theorem is Final Value Theorem. If f(t) and f′(t) are Laplace transformable, then