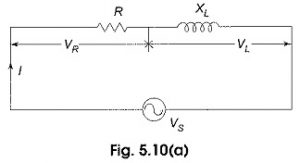
Principle of Superposition Theorem:

The Principle of Superposition Theorem states that in any linear network containing two or more sources, the response in any element is equal to the algebraic sum of the responses caused by individual sources acting alone, while the other sources are non-operative; that is, while considering the effect of individual sources, other ideal voltage sources and ideal current sources in the network are replaced by short circuit and open circuit across their terminals. This theorem is valid only for linear systems. This theorem can be better understood with a numerical example.

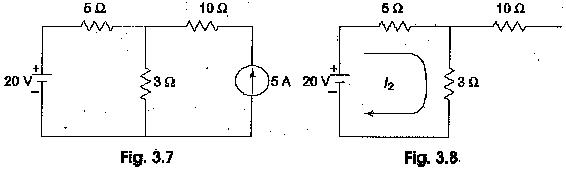
Consider the circuit which contains two sources as shown in Fig. 3.7.

Now let us find the current passing through the 3 Ω resistor in the circuit. According to Principle of Superposition Theorem, the current /₂ due to the 20 V Voltage source with 5 A source open circuited = 20/(5 + 3) = 2.5 A. (See Fig. 3.8)

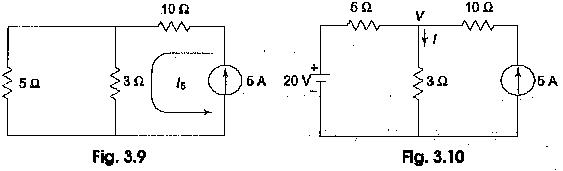
The current /₅ due to 5 A source with 20 V source short circuited is

The total current passing through the 3 Ω resistor is

Let us verify the above result by applying nodal analysis

The current passing in the 3 Ω resistor due to both sources should be 5.625 A. Applying nodal analysis to Fig. 3.10, we have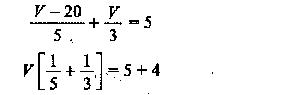

The current passing through the 3 Ω resistor is equal to V / 3

So the Principle of Superposition Theorem is verified. Let us now examine the power responses. Power dissipated in the 3 Ω resistor due to voltage source acting alone

Power dissipated  M the 3 Ω resistor due to current source acting alone

Power dissipated in the 3 Ω resistor when both the sources are acting simultaneously is given by

From the above results, the superposition of P₂₀ and P₅ gives

which is not equal to P = 94.92 W

We can, therefore, state that the superposition theorem is not valid for power responses. It is applicable only for computing voltage and current responses.