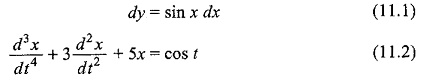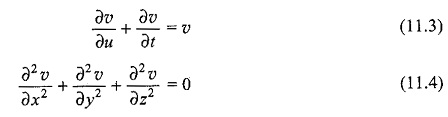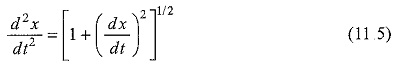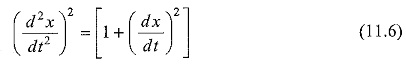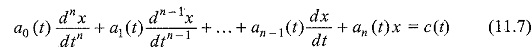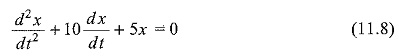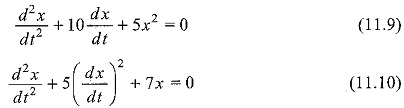Differential Equations Solutions and Basic Concepts:
Differential Equations Solutions and Basic Concepts which denote rates of change, occur in various branches of science and engineering. We make use of differential equations, for example, to determine the motion of a rocket or a satellite, to determine the charge or current in an electric circuit, or to determine the vibrations of a wire or membrane. The mathematical formulation of the above problems gives rise to differential equations.
A differential equation is one which involves derivatives of one or more dependent variables with respect to one or more independent variables. Differential equations are classified according to the variables and derivatives involved in them. Ordinary Differential Equations Solutions and Basic Concepts are those which involve ordinary derivatives of one or more dependent variables with respect to a single independent variable. For example
In Eq. 11.1, x is an independent variable, and y is a dependent variable. In Eq. 11.2, variable t is an independent variable and x is a dependent variable. Partial differential equations are those which involve partial derivatives of one or more dependent variables with respect to more than one independent variables. For example,
In Eq. 11.3, variables u and t are independent, and υ is a dependent variable.
In Eq. 11.4, variables x, y, and z are independent, whereas υ is a dependent variable.
The order of differential equation is the order of the highest derivative in it. Equation 11.1 is a first order differential equation, since the highest derivative involved is the first order. Similarly, Eq. 11.2 is of the 3rd order. Equations 11.3 and 11.4 are of the first and second order, respectively.
The degree of a differential equation is the degree of the derivative of the highest order; for example,
Equation 11.5 is of the second degree, since when the radical is removed, it becomes,
Differential Equations Solutions and Basic Concepts are further classified as linear and non-linear.
A linear ordinary differential equation of the order n, in the dependent variable x and the independent variable t, is given in the form
where a0 is not identically zero. The order of the equation is n. The term c(t) is the forcing function and is independent of x(t). When c(t) is zero, the equation is said to homogeneous; otherwise, it is non-homogeneous. A differential equation is said to be linear, when the dependent variable x and its derivatives occur in the first degree only, and no products of x and its derivatives are present in the equation.
For example,
In Eq. 11.8, the dependent variable, x, and its derivatives are of the first degree only. A non-linear ordinary differential equation is defined as an equation which is not linear,
For example,
In Eq. 11.7, if a0(t), a1(t) … an(t) are constants, the equation is said to be linear with constant coefficients; otherwise, the equation is said to be linear with variable coefficients.