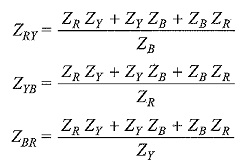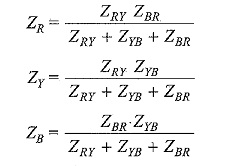Star Delta Transformation Formula:

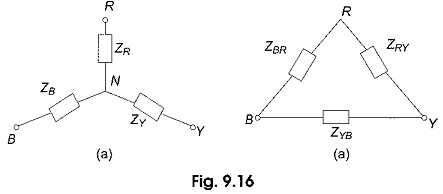
While dealing with currents and voltages in loads, it is often necessary to convert a Star Delta Transformation Formula, and vice-versa. It has already been seen that delta (Δ) connection of resistances can be replaced by an equivalent star (Y) connection and vice-versa. Similar methods can be applied in the case of networks containing general impedances in complex form. So also with ac, where the same formulae hold good, except that resistances are replaced by the impedances. These formulae can be applied even if the loads are unbalanced. Thus, considering Fig. 9.16(a), star load can be replaced by an equivalent delta-load with branch impedances as shown.

Delta impedances, in terms of star impedances, are

The converted network is shown in Fig, 9.16(b). Similarly, we can replace the delta load of Fig. 9.16(b) by an equivalent star load with branch impedances as

It should be noted that all impedances are to be expressed in their complex form.

Balanced Star-Delta and Delta-Star Conversion:

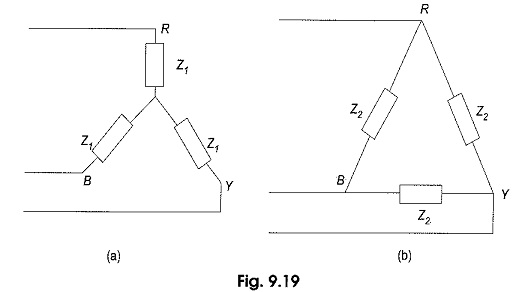
If the three-phase load is balanced, then the Star Delta Transformation Formula is shown below. Consider a balanced star-connected load having an impedance Z₁ in each phase as shown in Fig. 9.19(a).

Let the equivalent delta-connected load have an impedance of Z₂ in each phase as shown in Fig. 9.19(b). Applying the conversion formulae for delta impedances in terms of star impedances, we have

Similarly, we can express star impedances in terms of delta Z₁ = Z₂/3.