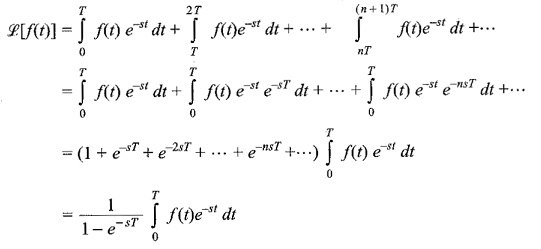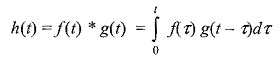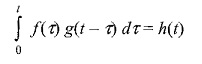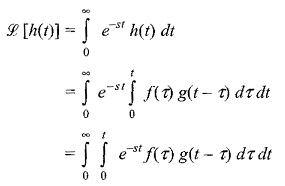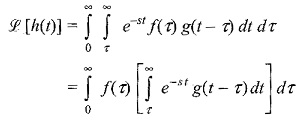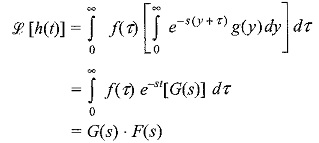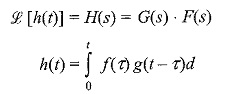Inverse Transformation:
We already discussed Laplace transforms of a functions f(t). If the function in frequency domain F(s) is given, the Inverse Transformation can be determined by taking the partial fraction expansion which will be recognizable as the transform of known functions.
Laplace Transform of Periodic Functions:
Periodic functions appear in many practical problems. Let function f(t) be a periodic function which satisfies the condition f(t) = f(t+T) for all t > 0 where T is period of the function.
The Convolution Integral:
If F(s) and G(s) are the Laplace transforms of f(t) and g(t), then the product of F(s) G(s) = H(s), where H(s) is the Laplace transform of h(t) given by f(t) *g(t) and defined by
Proof:
Let
By definition
By changing the order of integration of the above equation, we have
Put t – τ = y, and we get
Therefore,
τ defines the convolution of functions f(t) and g(t) and is expressed symbolically as
This theorem is very useful in frequency domain analysis.