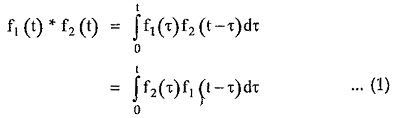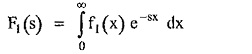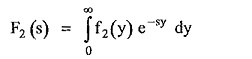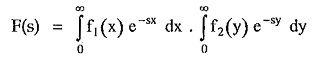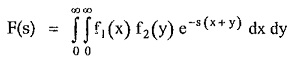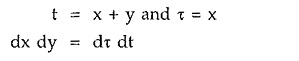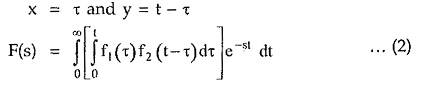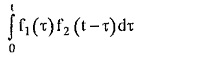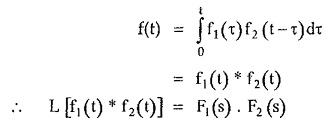Convolution Theorem:

The convolution theorem of Laplace transform states that, let f₁ (t) and f₂ (t) are the Laplace transformable functions and F₁ (s), F₂ (s) are the Laplace transforms of f₁ (t) and f₂ (t) respectively. Then the product of F₁ (s) and F₂ (s) is the Laplace transform of f(t) which is obtained from the convolution of f₁ (t) and f₂ (t). The convolution of f₁ (t) and f₂ (t) is denoted as f₁ (t) * f₂ (t) and is obtained by the equation,

where τ is the dummy variable.

where f₁ (t) * f₂ (t) indicates convolution of f₁ (t) and f₂ (t).

Proof:

Let

Where

x and y are dummy variables.

As x and y are independent variables we can write,

Consider the new variables t and τ such that,

Let us consider limits of integration interms of t and τ

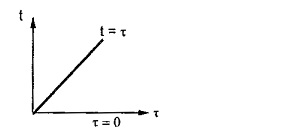
The smallest value of y is zero hence t ≥ τ.

The equation t = τ is straight line in t – τ plane. So to integrate area between the line t = τ and τ = 0, we get the limits for t as 0 →∞ while limits of τ as 0 to t.

Now

From the definition of Laplace transform the equation (2) represents Laplace transform of integral

which is called convolution integral. So in the equation (1),

Thus explained.