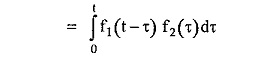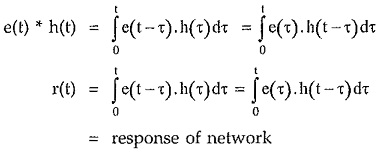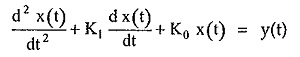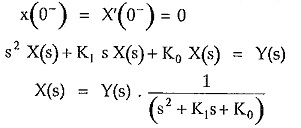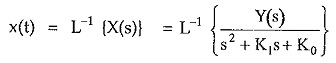Convolution Integral in Network Analysis:

The Convolution Integral in Network Analysis in Laplace transform states that

where f₁ (t) * f₂ (t) = Convolution of f₁ (t) and f₂ (t)

From the definition of system function,

Taking inverse Laplace,

From the convolution theorem,

where

Thus with the help of convolution of e(t) and h(t), the response of the network can be obtained directly.

Solving Differential Equations:

Consider the differential equation of order two, for simplicity of understanding as,

where K₁, K₀ are the constants.

We are interested to obtain the solution x(t) in time domain which satisfies the differential equation.

Take Laplace transform of both sides,

Let the initial conditions be zero for simplicity.

Assume

In this equation Y(s) is Laplace transform of y(t) which is known and called Forcing Function.

Hence taking Laplace inverse of X(s), using suitable method, the required solution can be obtained.

As most of the equations describing various networks are the differential equations, this technique is very effective in the network analysis. It takes into account, any initial conditions of the network as well.