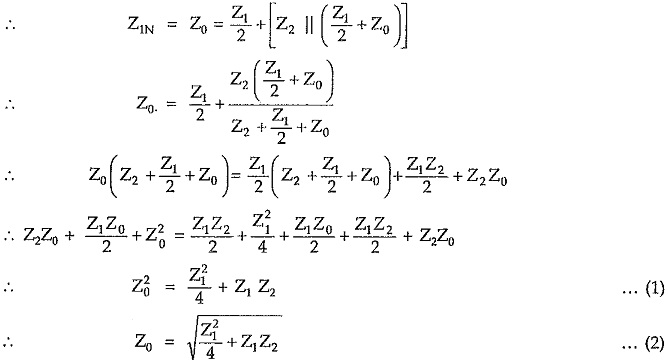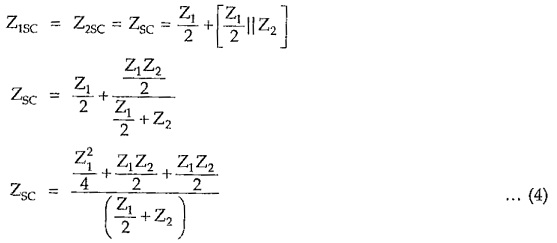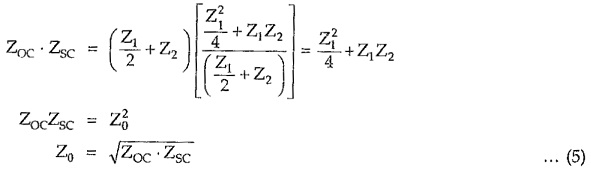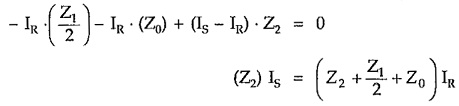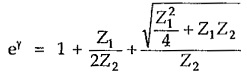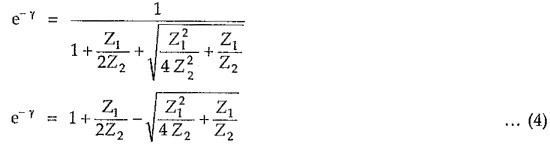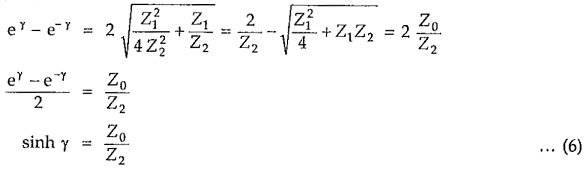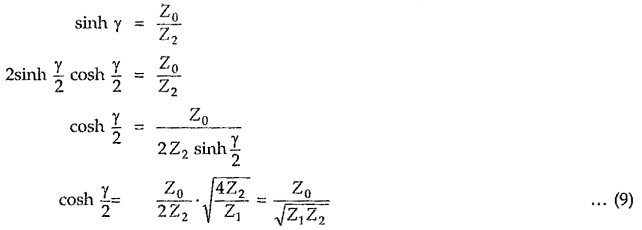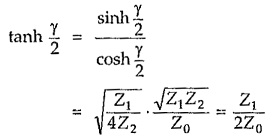Symmetrical T Network in Network Analysis:

In line transmission theory, the symmetrical T network is the most frequently used network. The condition in the symmetrical T network is that the total series arm impedance and shunt arm impedance must be Z₁ and Z₂ respectively. To have a total series arm impedance of Z_1^, the two series arm impedances must be selected as Z₁/2 each as shown in the Fig. 8.7.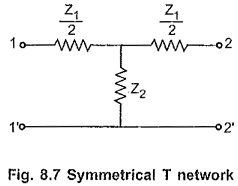

Let us derive the expressions for the characteristic impedance (Z₀) and propagation constant (γ) in terms of the network elements.

Characteristic Impedance (Z₀):

(A) In terms of series and shunt arm impedances

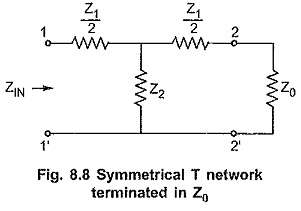
Consider a symmetrical T network terminated at its output terminal with its characteristic impedance as shown in the Fig. 8.8.

By the property of the symmetrical network, the input impedance of such network terminated in Z₀ at other port is equal to Z₀.

The input impedance of a T network is given by,

(B) In terms of open and short circuit impedances

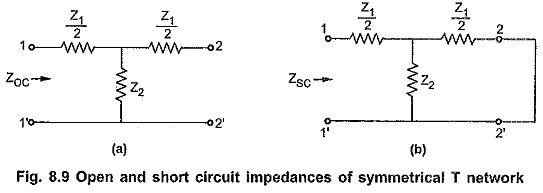
For symmetrical networks, impedances measured at any pair of terminals with other pair of terminals either open circuit or short circuit are of same value. Consider symmetrical T network with terminals 2-2′ either open circuit or short circuit as shown in the Fig. 8.9.

Consider Fig. 8.9 (a)^,

Consider Fig. 8.9 (b),

Multiplying equations (3) and (4), we can write,

Hence in any symmetrical network, the characteristic impedance Z₀ is the geometric mean of open and short circuit impedances measured at any pair of terminals.

Propagation Constant (γ):

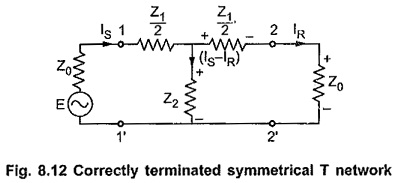
Consider properly terminated symmetrical T network as shown in the Fig. 8.12.

The currents entering and leaving network are assumed to be I_S and I_R respectively.

Applying KVL to the outer loop,

Hence

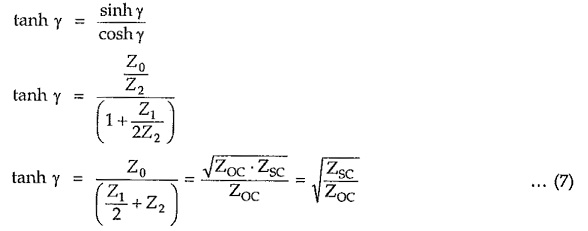
The propagation constant of T section is therefore given by

Putting value of Z₀ in equation (1), we can write,

From above equation we can write,

Adding equations (3) and (4), we get,

Subtracting equation (4) from (3), we get,

Dividing equation (6) by (5) we get,

Series and shunt arm impedances in terms of characteristic impedance (Z₀) and propagation constant (γ)

Consider equation (5),

Consider equation (6),

Dividing equation (8) and (9),

Thus each series arm impedance, in terms of the characteristic impedance and propagation constant is given by

Similarly, shunt arm impedance in terms of the characteristic impedance and propagation constant is given from equation (6) as

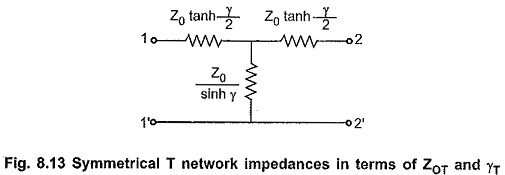
Hence T network with components expressed in terms of characteristic impedance and propagation constant is as shown in the Fig. 8.13.