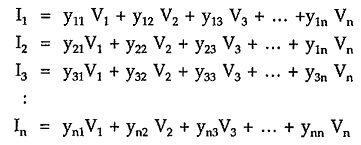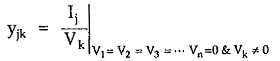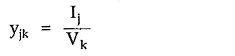Indefinite Admittance Matrix:

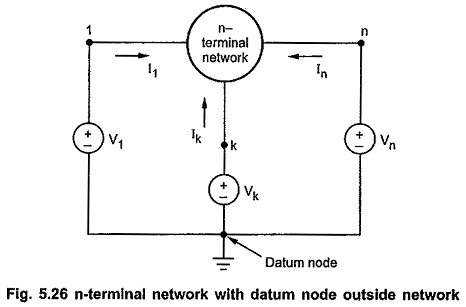
Consider Indefinite Admittance Matrix of a linear network with n terminals as shown in the Fig. 5.26.

Let us consider a zero potential reference node or datum node arbitrarily outside the n-terminal network. Let the voltage sources connected between the n-terminals of the network and datum node be V₁,V₂,V₃, … V_n. Let the currents entering the terminals be I₁,I₂,I₃, … I_n respectively.

As a network is linear and there are n voltage sources, we can apply superposition theorem for the calculation of current entering each terminal. The current entering each terminals is the partial combination of n sources. The currents are given by,

Above equations resemble short circuit admittance parameters, there is a basic difference between these parameters and the short circuit admittance parameters of a general two port network. The difference is that the parameters are calculated by considering datum node or reference node outside n-terminal network. Above equations can be written in matrix form as,

In general,

The matrix Y_i is known as indefinite admittance matrix.

Let y_jk be the element of Y_i and it is given by

The parameter y_jk is the ratio of current entering j^th terminal when all the node are shorted to reference node except k^th node to the voltage at k^th node. To determine y_jk,

• Short all the terminals to datum node except the terminal k.
• Connect known voltage source V_k between k^th terminal and datum node.
• Measure current entering j^th terminal as I_j and find ratio

Properties:

The properties of indefinite admittance matrix are as follows,

• The sum of the elements of every column of an indefinite admittance matrix is zero.
• The sum of the elements of every row of an indefinite matrix is zero.
• If an isolated node is added to n-terminal network then the order of indefinite admittance matrix becomes (n + 1) x (n + 1) and it is obtained by adding a row and column of zeros to n x n matrix of original network.
• The value of determinant of indefinite admittance matrix is zero.
• For a reciprocal n-terminal network, indefinite admittance matrix is symmetric.
• If any one the nodes of n-terminal network is made reference node, then the row and the column corresponding to that terminal may be removed from the indefinite admittance matrix.