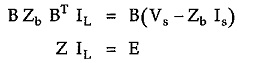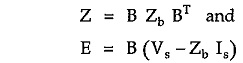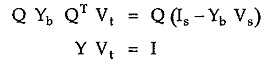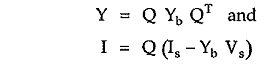Network Equilibrium Equation in Matrix Form:

In earlier section we have studied how to obtain equilibrium equations for a network which are based on loop analysis and node analysis. We can represent the same Network Equilibrium Equation in Matrix Form which simplifies the task of analysis of a large scale network.

Loop or Mesh or KVL Equilibrium Equations:

The KVL equilibrium equations based on loop or mesh analysis are given by

where

The quantities involved in above equations are as follows.

B is the f circuit or tie-set matrix of order (b – n+1) x b,

Z_b is the branch impedance matrix of order b x b,

I_L is the column matrix of loop currents of order (b – n + 1) x 1

V_s is the column matrix of voltage sources of order b x 1.

I_s is column matrix of source currents of order b x 1

Z is coefficient matrix also known as loop impedance matrix of order (b – n +1) x (b – n +1)

E is the column matrix of order (b – n +1) x 1 which represents voltages in loop.

The matrix equation ZI_L = E represents a set of (b – n + 1) independent loop equations for a network with n nodes and b branches.

Node or KCL Equilibrium Equation:

The KCL equilibrium equations based on nodal analysis are given by

where

The quantities involved in above equations are as follows.

Q is the f-cutset matrix of order (n -1) x b

Y_b is branch admittance matrix of order b x b

V_t is column matrix of tree branch voltages of order (n -1) x 1

I_s is the column matrix of branch input current sources of order b x 1

V_s is column matrix of branch input voltage sources

Y is node admittance matrix of order (n -1) x (n -1)

I is the column matrix of order (n -1) x 1 which represents algebraic sum of current sources.