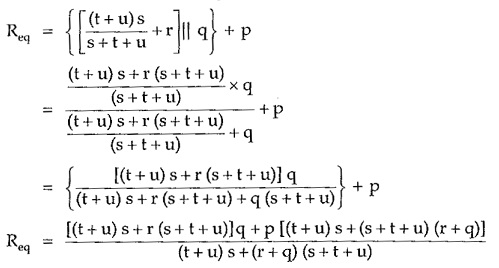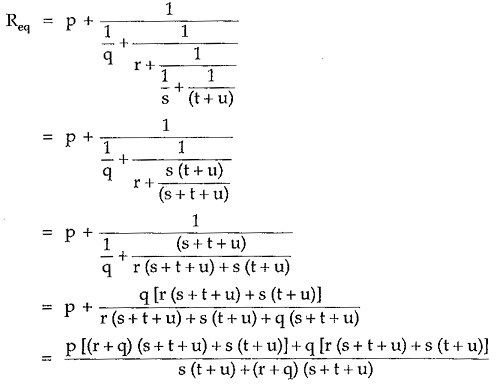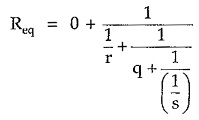Ladder Network Circuit Analysis:
By using this Ladder Network Circuit Analysis, we can find the equivalent resistance by Continued Fractions Method.
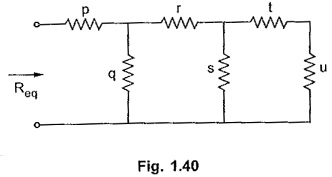
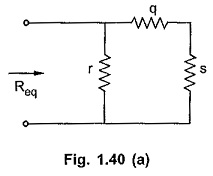
Consider a Ladder Network Circuit as shown in the Fig. 1.40.
Let us calculate equivalent resistance by series parallel method first.
So (t + u) is in parallel with s. The combination is in series with r. The entire combination is in parallel with q and finally equivalent of the combination is in series with p, to get Req.
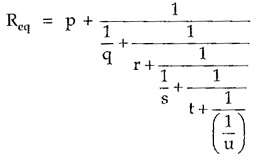
Instead of doing these calculations, in Continued Fractions Method, the resistances of the ladder network are written in a particular fraction form. According to this method, Req of the above network can be directly written as,
It can be observed that all the horizontal branch resistances appear as it is, in the fraction from while the vertical branch resistances appear as the reciprocals in this form. Solving this fractional form Req can be obtained.
This is same as obtained above by series parallel method.
Note that if resistance p is absent in the Ladder Network as shown in the Fig. 1.40(a) then it must be treated as a resistance of zero ohms in the first horizontal branch. And in such case, Continued Fractions Method is written as,
Remember that horizontal branch resistances appear as it is while vertical branch resistances appear in the reciprocal form, in this method.