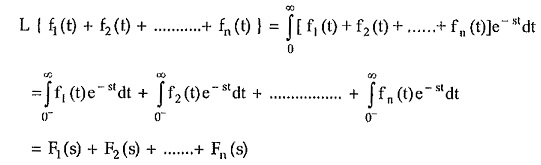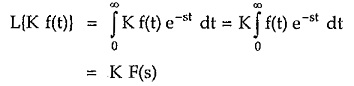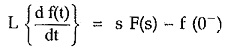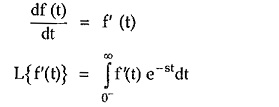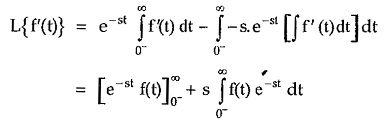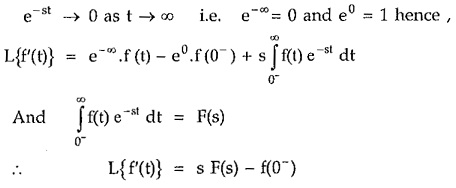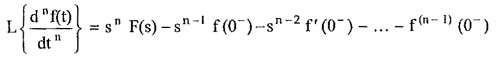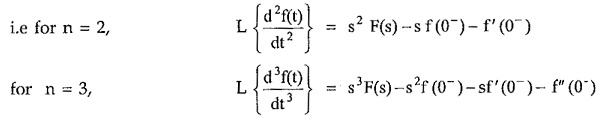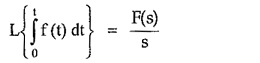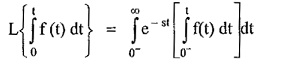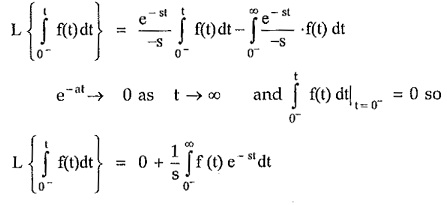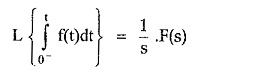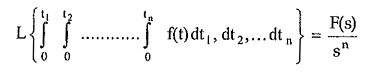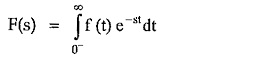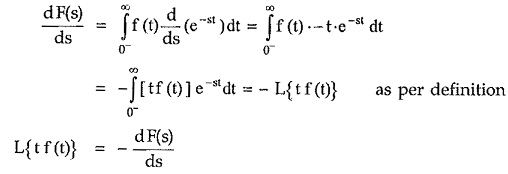Laplace Transform Properties:

The Laplace Transform Properties are namely,

1. Linearity:

The transform of a finite sum of time functions is the sum of the Laplace transforms of the individual functions.

So if F₁(s), F₂(s),……..F_n(s) are the Laplace transforms of the time functions f₁(t), f₂(t), ……….., f_n(t) respectively then,

Explain: Let us find the Laplace transform of the sum from the basic definition.

The property can be further extended if the time functions are multiplied by the constants i.e.

where a₁,a₂,……..,a_n are constants.

2. Scaling Theorem:

If K is a constant then the Laplace transform of Kf(t) is given as K times the Laplace transform of f(t).

This can be proved very easily. According to definition,

3. Real Differentiation (Differentiation in Time Domain):

Another Laplace Transform Properties is Real Differentiation. Let F(s) be the Laplace transform of f(t). Then,

where f (0^–) indicates value of f(t) at t = 0^– i.e. just before the instant t = 0

Explain : The real differentiation is denoted as,

Integrating the right hand side by parts,

The theorem can be extended for n^th order derivative as,

where f^(n-1)(0^–) is the value of (n – 1)^th derivative of f(t) at t = 0^–.

This property is most useful as it transforms differential time domain equations to simple algebraic equations, alongwith the initial conditions, if any.

4. Real Integration:

If F(s) is the Laplace transform of f(t) then,

Explain : By the definition,

Integrating the right hand side by parts,

This property can be extended for multiple integrals as,

5. Differentiation by s:

If F(s) is the Laplace transform of f(t) then the differentiation by s in the complex frequency domain corresponds to the multiplication by t in the time domain.

Explain : From the definition of the Laplace transform, F(s) = f f (t) e’dt

Differentiating both sides with respect to s,

6. Complex Translation:

Another Laplace Transform Properties is Complex Translation. If F(s) is the Laplace transform of f(t) then by the complex translation property,

where a is the complex number

7. Real Translation (Shifting Theorem):

This theorem is useful to obtain the Laplace transform of the shifted or delayed function of time.

If F(s) is the Laplace transform of f(t) then the Laplace transform of the function delayed by time T is,

8. Initial Value Theorem:

The Laplace transform properties is very useful to find the initial value of the time function f(t). Thus if F(s) is the Laplace transform of f(t) then,

The only restriction is that f(t) must be continuous or at the most, a step discontinuity at t = 0.

9. Final Value Theorem:

Similar to the initial value, the Laplace transform is also useful to find the final value of the time function f(t). Thus if F(s) is the Laplace transform of f(t) then the final value theorem states that,

The only restriction is that the roots of the denominator polynomial of F(s) i.e. poles of F(s) have negative or zero real parts.